Sign in Subscribe
12 min read

Higher Kinds in C# with language-ext [Part 3 - foldables]

Foldables abstract the idea of aggregation away from simple lists (like Aggregate in LINQ) to many other types.
Higher Kinds in C# with language-ext [Part 3 - foldables]

This is a multi-part series of articles, it's worth going back to the earlier parts if you haven't read them already:

And "yes", this time the artwork is my own. And whilst I'm no Kandinsky, he's not as good at functional-programming as me, so I guess we're even!

In part two we showed that by defining a separate trait-implementation type we could make a data-type (like List<A> and Maybe<A>) into a functor. Functors require higher-rank polymorphism to work, and we made it work. Yay!

Let's just do one more Functor type: Either<L, R>. Either<L, R> is a little more interesting, because it has two generic-parameters, whereas List<A> and Maybe<A> have only one. 

// Data-types
public abstract record Either<L, R> : K<Either<L>, R>;
public record Left<L, R>(L Value) : Either<L, R>;
public record Right<L, R>(R Value) : Either<L, R>;

// Trait implementation
public class Either<L> : Functor<Either<L>>
{
    public static K<Either<L>, B> Map<A, B>(K<Either<L>, A> ma, Func<A, B> f) =>
        ma.As() switch
        {
            Left<L, A> (var l) => new Left<L, B>(l),
            Right<L, A> (var r) => new Right<L, B>(f(r))
        };
}

// Extensions that provides the down-casting
public static class EitherExtensions
{
    public static Either<L, R> As<L, R>(this K<Either<L>, R> ma) =>
        (Either<L, R>)ma;
}

It should be relatively clear now that the trait-implementation should just have the last generic parameter removed. So, Either<L, R> becomes Either<L>, Maybe<A> becomes Maybe, etc.

If you think about it, this is a little bit like how partial-application works with functions. But, because C# won't allow us to partially apply Either<L, R> by just providing the L – we need a second type that is partially-applied. That second type completes its application, not by getting all its arguments from the type, but by moving the final argument from the type-signature to the method signatures. The methods within the partially-applied trait-implementation provide the final argument. This is the key to the technique.

Let's look at another higher-kind now: Foldable. Foldables are aggregators and usually provide two methods: Fold and FoldBack – sometimes called FoldRight and FoldLeft, but in language-ext we use the Fold and FoldBack parlance. For, the uninitiated, Fold is the same as Aggregate in LINQ (first item to last item aggregation); FoldBack is like doing the aggregation in reverse: last item to first.

public interface Foldable<T> 
    where T : Foldable<T>
{
   public static abstract S Fold<A, S>(K<T, A> ta, S initial, Func<S, A, S> f);

   public static abstract S FoldBack<A, S>(K<T, A> ta, S initial, Func<S, A, S> f);
}

And, just like Select before, we can add our one-and-only implementation of the Fold and FoldBack extension methods:

public static S Fold<T, A, S>(this K<T, A> ta, S initial, Func<S, A, S> f)
    where T : Foldable<T> =>
    T.Fold(ta, initial, f);

public static S FoldBack<T, A, S>(this K<T, A> ta, S initial, Func<S, A, S> f)
    where T : Foldable<T> =>
    T.FoldBack(ta, initial, f);
By the way, we don't actually need to write these extension methods, they just make working with the traits more convenient.

Now we can get the three trait types we've made so far List, Maybe, and Either<L> and make them foldable...

List

public record List : 
    Functor<List>,
    Foldable<List>
{
    public static K<List, B> Map<A, B>(K<List, A> xs, Func<A, B> f) =>
        new List<B>(xs.As().Items.Select(f).ToArray());

    public static S Fold<A, S>(K<List, A> xs, S initial, Func<S, A, S> f) =>
        xs.As().Items.Aggregate(initial, f);

    public static S FoldBack<A, S>(K<List, A> xs, S initial, Func<S, A, S> f) =>
        xs.As().Items.Reverse().Aggregate(initial, f);
}

Maybe


public class Maybe : 
    Functor<Maybe>,
    Foldable<Maybe>
{
    public static K<Maybe, B> Map<A, B>(K<Maybe, A> ma, Func<A, B> f) =>
        ma.As() switch
        {
            Just<A> (var x) => new Just<B>(f(x)),
            Nothing<A>      => new Nothing<B>()
        };

    public static S Fold<A, S>(K<Maybe, A> ma, S initial, Func<S, A, S> f) =>
        ma.As() switch
        {
            Just<A> (var x) => f(initial, x),
            Nothing<A>      => initial
        };

    public static S FoldBack<A, S>(K<Maybe, A> ma, S initial, Func<S, A, S> f) =>
        Fold(ma, initial, f);
}

Either<L>


public class Either<L> : 
    Functor<Either<L>>,
    Foldable<Either<L>>
{
    public static K<Either<L>, B> Map<A, B>(K<Either<L>, A> ma, Func<A, B> f) =>
        ma.As() switch
        {
            Left<L, A> (var l)  => new Left<L, B>(l),
            Right<L, A> (var r) => new Right<L, B>(f(r))
        };

    public static S Fold<A, S>(K<Either<L>, A> ma, S initial, Func<S, A, S> f) =>
        ma.As() switch
        {
            Left<L, A>          => initial,
            Right<L, A> (var r) => f(initial, r),
        };

    public static S FoldBack<A, S>(K<Either<L>, A> ma, S initial, Func<S, A, S> f) =>
        Fold(ma, initial, f);
}
We still haven't modified the List<A>, Maybe<A>, or Either<L, R> types directly. We're just extending the set of capabilities via the trait-implementions.

When we made our types into functors they gained the ability to Map, but nothing else really. So, it was a fair amount of typing to not get much in return. Foldable is quite different. Let's see what we can give any type that implements Foldable.

First up, let's count the items in any foldable:

public static int Count<T, A>(this K<T, A> ta)
    where T : Foldable<T> =>
    ta.Fold(0, (s, _) => s + 1);

Next, we can sum the items in any foldable, with any numeric bound-value:

public static A Sum<T, A>(this K<T, A> ta)
    where T : Foldable<T> 
    where A : INumber<A> =>
    ta.Fold(A.Zero, (s, x) => s + x);

We can see if any foldable is empty:

public static bool IsEmpty<T, A>(this K<T, A> ta)
    where T : Foldable<T> =>
    ta.Fold(true, (_, _) => false);

If the bound-value type is monoidal then we can use that to aggregate using the monoid's associative operator:

public static A Fold<T, A>(this K<T, A> ta)
    where T : Foldable<T>
    where A : Monoid<A> =>
    ta.Fold(A.Empty, (s, x) => s + x);

We can convert any foldable into an IEnumerable:

public static IEnumerable<A> AsEnumerable<T, A>(this K<T, A> ta)
    where T : Foldable<T>
{
    var list = new System.Collections.Generic.List<A>();
    return ta.Fold(list, (s, x) =>
    {
        s.Add(x);
        return s;
    });
}

We can implement more of the standard LINQ operators (without 'magic methods'):

// Returns true if the predicate holds for all items
public static bool All<T, A>(this K<T, A> ta, Func<A, bool> f)
    where T : Foldable<T> =>
    ta.Fold(true, (s, x) => s && f(x));

// Returns true if the predicate holds for any item
public static bool Any<T, A>(this K<T, A> ta, Func<A, bool> f)
    where T : Foldable<T> =>
    ta.Fold(false, (s, x) => s || f(x));

And we can check if a known item is within any foldable structure:

public static bool Contains<T, A>(this K<T, A> ta, A value)
    where A : IEquatable<A>
    where T : Foldable<T> =>
    ta.Any(x => x.Equals(value));
These functions are written just once. And they work for List<A>, Maybe<A>, and Either<L, R> automatically. They will also work for any foldable you write! Yay, free code!

Now, some of the more performance minded individuals reading this might think "Er, but these methods do more work than they need to". And, you'd be right. For example, the IsEmpty method has to traverse every item in the foldable, even though you know on the first item if it's empty or not. Count traverses every item also, yet List<A> has an internal representation that is an array – it knows how many items there are without walking the collection.

We fix this by moving these methods into Foldable and making them default implementations that can be overridden where desired.

New Foldable<T> trait:

public interface Foldable<T> 
    where T : Foldable<T>
{
    // Abstract members that everyone has to implement

    public static abstract S Fold<A, S>(K<T, A> ta, S initial, Func<S, A, S> f);

    public static abstract S FoldBack<A, S>(K<T, A> ta, S initial, Func<S, A, S> f);
    
    // Virtual members with useful default implementations

    public static virtual bool IsEmpty<A>(K<T, A> ta) =>
        T.Fold(ta, true, (_, _) => false);

    public static virtual int Count<A>(K<T, A> ta) =>
        T.Fold(ta, 0, (s, _) => s + 1);

    public static virtual A Sum<A>(K<T, A> ta)
        where A : INumber<A> =>
        T.Fold(ta, A.Zero, (s, x) => s + x);

    public static virtual A Fold<A>(K<T, A> ta)
        where A : Monoid<A> =>
        T.Fold(ta, A.Empty, (s, x) => s + x);

    public static virtual IEnumerable<A> AsEnumerable<A>(K<T, A> ta)
    {
        var list = new System.Collections.Generic.List<A>();
        return ta.Fold(list, (s, x) =>
        {
            s.Add(x);
            return s;
        });
    }

    public static virtual bool All<A>(K<T, A> ta, Func<A, bool> f) =>
        T.Fold(ta, true, (s, x) => s && f(x));

    public static virtual bool Any<A>(K<T, A> ta, Func<A, bool> f) =>
        T.Fold(ta, false, (s, x) => s || f(x));

    public static virtual bool Contains<A>(K<T, A> ta, A value)
        where A : IEquatable<A> =>
        T.Any(ta, x => x.Equals(value));    
}

Note, how the methods we've moved into Foldable are static virtual – which means we can override them in our trait-implementations. But, if we don't, we still get the free functionality. The default implementations happen to be pretty optimial for Maybe and Either – they could be better, but's probably not worth the effort to provide hand-written overrides; but for List we should definitely do some manual overrides if we want to get the best performance.

Updated List trait-implementation with optimised overrides:

public record List : 
    Functor<List>,
    Foldable<List>
{
    public static K<List, B> Map<A, B>(K<List, A> xs, Func<A, B> f)
    {
        // Optimises by pre-allocating the array before mapping
        var items = xs.As().Items;
        var bs = new B[items.Length];
        var ix = 0;
        foreach(var item in items)
        {
            bs[ix] = f(item);
            ix++;
        }
        return new List<B>(bs);
    }

    public static S Fold<A, S>(K<List, A> xs, S state, Func<S, A, S> f)
    {
        // Optimises by running as a simple imperative for-loop
        foreach(var item in xs.As().Items)
        {
            state = f(state, item);
        }
        return state;
    }

    public static S FoldBack<A, S>(K<List, A> xs, S state, Func<S, A, S> f)
    {
        // Optimises by running an imperative for-loop backwards 
        var items = xs.As().Items;
        for (var ix = items.Length - 1; ix >= 0; ix--)
        {
            state = f(state, items[ix]);
        }
        return state;
    }

    public static bool IsEmpty<A>(K<List, A> ta) =>
        // Optimises by using the known length of the array 
        ta.As().Items.Length == 0;

    public static int Count<A>(K<List, A> ta) =>
        // Optimises by using the known length of the array 
        ta.As().Items.Length;

    public static IEnumerable<A> AsEnumerable<A>(K<List, A> ta) =>
        // Optimises by passing the array back directly 
        ta.As().Items;

    public static bool All<A>(K<List, A> ta, Func<A, bool> f)
    {
        // Optimises by turning into a simple loop that can bail out early
        foreach (var item in ta.As().Items)
        {
            if (!f(item)) return false;
        }
        return true;
    }

    public static bool Any<A>(K<List, A> ta, Func<A, bool> f)
    {
        // Optimises by turning into a simple loop that can bail out early
        foreach (var item in ta.As().Items)
        {
            if (f(item)) return true;
        }
        return false;
    }
}
What's really nice about this is that we can 'get moving' and write our code to leverage these higher-kinded types and gain all of this functionality and then come back later to provide more optimal solutions. The definition of not optimising prematurely.

We should update the extension methods to use these new trait methods too. Here's the full set of extensions so far:

public static class TraitExtensions
{
    public static K<F, B> Select<F, A, B>(this K<F, A> fa, Func<A, B> f)
        where F : Functor<F> =>
        F.Map(fa, f);
    
    public static K<F, B> Map<F, A, B>(this K<F, A> fa, Func<A, B> f)
        where F : Functor<F> =>
        F.Map(fa, f);

    public static S Fold<T, A, S>(this K<T, A> ta, S initial, Func<S, A, S> f)
        where T : Foldable<T> =>
        T.Fold(ta, initial, f);

    public static S FoldBack<T, A, S>(this K<T, A> ta, S initial, Func<S, A, S> f)
        where T : Foldable<T> =>
        T.Fold(ta, initial, f);

    public static bool IsEmpty<T, A>(this K<T, A> ta)
        where T : Foldable<T> =>
        T.IsEmpty(ta);

    public static int Count<T, A>(this K<T, A> ta)
        where T : Foldable<T> =>
        T.Count(ta);

    public static A Sum<T, A>(this K<T, A> ta)
        where T : Foldable<T> 
        where A : INumber<A> =>
        T.Sum(ta);

    public static A Fold<T, A>(this K<T, A> ta)
        where T : Foldable<T>
        where A : Monoid<A> =>
        T.Fold(ta);

    public static IEnumerable<A> AsEnumerable<T, A>(this K<T, A> ta)
        where T : Foldable<T> =>
        T.AsEnumerable(ta);

    public static bool All<T, A>(this K<T, A> ta, Func<A, bool> f)
        where T : Foldable<T> =>
        T.All(ta, f);

    public static bool Any<T, A>(this K<T, A> ta, Func<A, bool> f)
        where T : Foldable<T> =>
        T.Any(ta, f);

    public static bool Contains<T, A>(this K<T, A> ta, A value)
        where A : IEquatable<A>
        where T : Foldable<T> =>
        T.Contains(ta, value);
}

It is clear from this that we don't have to forego performance to leverage more abstract compositional capabilities. These methods will be as fast as any handwritten code and yet we can write abstract functions that work with any foldables and any functors; yet when they're consumed they run the highly optimised trait implementations, not some generic code that has no understanding of the underlying type.

Contrast that with IEnumerable<T>, which, once your collection-type has been cast to from its concrete type, like List<T>, to its abstract representation of IEnumerable<T>, instantly becomes opaque – with the only access to the underlying type being its ability to yield an enumerator. Yet, we have a ton of extension methods hanging off the type that are completely clueless to what's underneath. There are no such issues with the higher-kinds + traits approach!

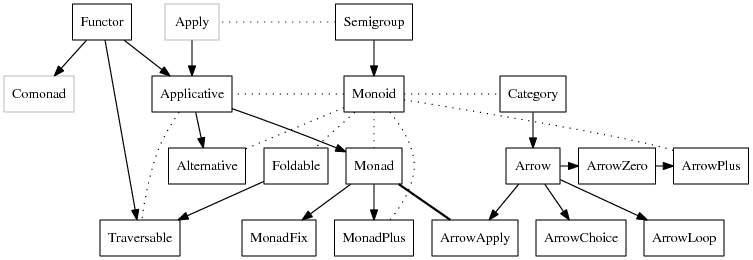
On the Haskell wiki is what's known as the 'Typeclassopedia'. So far, we've covered:

  • Semigroup
  • Monoid
  • Foldable
  • Functor
  • and mentioned in passing: Applicative and Traversable

Can you guess where we're going next?

Part 4

Published by:

Paul Louth