Higher Kinds in C# with language-ext [Part 4 - applicatives]

This is a multi-part series of articles, it's worth going back to the earlier parts if you haven't read them already:

• Part 1 - Introduction, traits, semigroups, and monoids
• Part 2 - Functors
• Part 3 - Foldables

Since the last article I've released an early alpha of language-ext. The alpha contains all of the trait-types in this series – so if you feel like 'skipping ahead' then feel free to have a look. Just remember that it's not ready for production yet!

Anyway, let's now look at the next trait-type: ‘Applicatives’. Or, to give them their full name: Applicative Functors.

Applicative Functors are a 'stepping stone' between functors and monads – they're probably less well-known but have some interesting properties of their own when it comes to lifted expression evaluation. Two of the major uses in language-ext is to enable automatic parallel processing of effectful computations and to automatically collect multiple errors when validating. Those aren't the only usages – all of the higher-kinded-types, including the collection-types, have the applicative traits.

If we take a look back at Functor, it has a single method in its trait: Map. Map takes a regular function Func<A, B> and allows it to run on the bound-values within the functor, effectively making a Func<A, B> into a Func<F<A>, F<B>>.

For example, if I have an A then a Func<A, B> will get me a B. This is basic stuff. But, if I have one or more A values within an F<A>, I want to be able to apply the Func<A, B> to the bound values to transform them: that's what Map does. It means that every function that's ever been written to work with single values of A can now work with any type that is a 'container' of zero or more values of A.

So, for List<A> we get to turn it into a List<B> by applying Func<A, B> with Map.

The function passed to map has a single argument - it's a unary operation. So, simple operations like this are easily achievable:

// Simple unary function
static bool Not(bool x) =>
    !x; 

// Mapping of a list of booleans
var xs = new List<bool>([true, false, true]);
var ys = xs.Map(Not);

// Mapping a boolean Maybe
var mx = new Just<bool>(true);
var my = mx.Map(Not);

What happens if we want to do a binary operation? How would we achieve that?

Let's take a look at a simple mathematical expression:

1 × 2 + 3 × 4

What if the operands weren't just pure values, but were instead lifted up into a Maybe?

Just(1) * Just(2) + Just(3) * Just(4)

Could we still operate on those values without losing the semantics of the Maybe structure – namely that the values are optional?

If the values were int? then we may write some code like this:

int? w = ...;
int? x = ...;
int? y = ...;
int? z = ...;

if(w.HasValue && 
   x.HasValue && 
   y.HasValue && 
   z.HasValue)
{
   return w.Value * x.Value + y.Value * z.Value;
}
else
{
   return null;
}

Plenty of boilerplate and plenty of opportunities to make a mistake.

WARNING: This next section is becomes a bit of a mindfuck before it gets good. Stick with it!

With Maybe<int> what could we do? So far, we've only got support for Map and Fold behaviours. Map takes unary function arguments, but we have binary functions (+ and ×), how can we make them unary? Simply, we can curry them:

// Binary addition function
static int Add(int x, int y) =>
    x + y; 

// Binary multiplication function
static int Multiply(int x, int y) =>
    x * y; 

// Curry the functions
var add = curry<int, int, int>(Add);           // (int x) => (int y) => x + y
var multiply = curry<int, int, int>(Multiply); // (int x) => (int y) => x * y

Currying creates a series of nested lambdas rather than a single 'tuple' lambda. This allows us to partially apply our arguments to the functions.

var add10 = add(10);      // Func<int, int>
var result = add10(20);   // 30

Partial application allows us to progressively feed values into the function without the need to collect all of the argument the values upfront.

Let's now create the four terms of our expression:

var mw = new Just<int>(1);
var mx = new Just<int>(2);
var my = new Just<int>(3);
var mz = new Just<int>(4);

And then start multiplying with Map:

K<Maybe, Func<int, int>> r1 = mw.Map(multiply);

What we end up here is the value inside mw being partially applied to the multiply function – it returns a function that gets wrapped back up inside a Maybe<Func<int, int>> – if we can just supply one more argument then we have the first multiplication expression done:

var r2 = r1.Map(f => mx.Map(f));   // K<Maybe, K<Maybe, int>>

So, we call Map on r1 (which has a Func<int, int> inside), we then pass that to mx.Map – which completes the multiplication operation.

But, we have problem! We want our Map operation to be int → int, we were not expecting another Maybe<int> to be returned. However, because of our nesting of Mapoperations we cause the final r2 result to be two nested maybes. This isn't good!

If we take it further and try to do the full expression: 1 x 2 + 3 x 4 then it gets worse!

var lhs = mw.Map(multiply).Map(f => mx.Map(f));
var rhs = my.Map(multiply).Map(f => mz.Map(f));
var res = lhs.Map(l => l.Map(add).Map(f => rhs.Map(r => r.Map(f))));

Would you like to guess what res is? You got it:

K<Maybe, K<Maybe, K<Maybe, K<Maybe, int>>>> res;  // Ouch!

Four nested maybes! So, not only do we not have the result we want, it's truly horrible to write. We need a better solution, we need applicative functors!

public interface Applicative<F> : Functor<F>
    where F : Applicative<F>
{
    public static abstract K<F, A> Pure<A>(A value);

    public static abstract K<F, B> Apply<A, B>(K<F, Func<A, B>> mf, K<F, A> ma);
}

Take a look at the Apply function signature. Does is remind you of anything? Let's take a look at Functor again:

public interface Functor<F>  
    where F : Functor<F>
{
    public static abstract K<F, B> Map<A, B>(Func<A, B> f, K<F, A> ma);
}

By the way, I am now using the definition from language-ext, where K<F, A> is the last argument in the argument-list for Map.

Both Map and Apply look almost exactly the same. The only difference is that the Func<A, B> is also lifted in the applicative Apply function (i.e. it's wrapped up in a K<F, ...>).

But, if you look at the, earlier, first step of trying to partially-apply the mulitply function:

K<Maybe, Func<int, int>> r1 = mw.Map(multiply);

Then you'll notice that it too is a Func that is lifted into the Maybe structure. Looks like we might be on something here!

Let's implement Applicative for Maybe:

public class Maybe : 
    Foldable<Maybe>,
    Applicative<Maybe>
{
    public static K<Maybe, A> Pure<A>(A value) =>
        new Just<A>(value);

    public static K<Maybe, B> Apply<A, B>(K<Maybe, Func<A, B>> mf, K<Maybe, A> ma) =>
        mf switch
        {
            Just<Func<A, B>> (var f) => 
                ma switch
                {
                    Just<A>(var a) =>
                        new Just<B>(f(a)),
                    
                    Nothing<A> =>
                        new Nothing<B>()
                },
            Nothing<Func<A, B>> =>
                new Nothing<B>()
        };
    
    public static K<Maybe, B> Map<A, B>(Func<A, B> f, K<Maybe, A> ma) =>
        ma switch
        {
            Just<A> (var x) => new Just<B>(f(x)),
            Nothing<A>      => new Nothing<B>()
        };
    
    public static S FoldWhile<A, S>(
        Func<A, Func<S, S>> f,
        Func<(S State, A Value), bool> predicate,
        S state,
        K<Maybe, A> ta) =>
        ta switch
        {
            Just<A> (var x) when predicate((state, x)) => f(x)(state),
            _                                          => state
        };
    
    public static S FoldBackWhile<A, S>(
        Func<S, Func<A, S>> f, 
        Func<(S State, A Value), bool> predicate, 
        S state, 
        K<Maybe, A> ta) =>
        Fold(s => a => f(a)(s), state, ta);
}

I have implemented the traits as they exist in language-ext. So, you'll notice the new implementation of Map reflects the interface in language-ext, rather than the implementations from the earlier articles. Additionally, you should see that Fold and FoldBack are now FoldWhile and FoldWhileBack – these are the actual abstract methods used in the language-ext interface: it allows for more optimal default implementations of the other trait methods, like Exists, ForAll, IsEmpty, etc.

Let's look at the implementation of Apply:

public static K<Maybe, B> Apply<A, B>(K<Maybe, Func<A, B>> mf, K<Maybe, A> ma) =>
    mf switch
    {
        Just<Func<A, B>> (var f) => 
            ma switch
            {
                Just<A>(var a) =>
                    new Just<B>(f(a)),
                
                Nothing<A> =>
                    new Nothing<B>()
            },
        Nothing<Func<A, B>> =>
            new Nothing<B>()
    };

It's a simple nested pattern-match that tries to extract the Func<A, B> from mf and the A from ma. If either of them are in a Nothing state then we get Nothing returned. Which makes sense – we can't invoke the function if we don't have the function or if we don't have the argument to pass to the function.

But, if both mf and ma are in a Just state then we can simply invoke the function and then wrap it back up inside a Maybe by passing the result to the constructor for Just.

Let's update our extension methods to allow us to use the new applicative Apply method. We'll also add a new Map extension with the arguments flipped (I mentioned in an earlier episode that I would demonstrate why the arguments are flipped – you're about to see why it works this way):

// Functor map (notice that `this` is a `Func`)
public static K<F, B> Map<F, A, B>(this Func<A, B> f, K<F, A> ma) 
    where F : Functor<F> =>
    F.Map<A, B>(f, ma);

// Applicative apply
public static K<F, B> Apply<F, A, B>(this K<F, Func<A, B>> mf, K<F, A> ma) 
    where F : Applicative<F> =>
    F.Apply<A, B>(mf, ma);

If you remember our first attempt at multiplying two Maybe<int> values together looked like this:

var r = mw.Map(multiply).Map(f => mx.Map(f));

And that resulted in a nested Maybe<Maybe<int>>. Instead, we can now use the Apply function (along with the flipped-argument Map) to avoid the nesting:

var r = multiply.Map(mw).Apply(mx)   // K<Maybe, int>

And that works! Returning a K<Maybe, int> rather than the double-nested maybe we saw earlier. The flipped-argument Map function also allows us to move the function-argument to the left-most position in the expression, it is then followed by n arguments that are fluently fed into the function. This just reads better.

For those that know Haskell, you'll recognise this technique. In Haskell it would look like this:

let r = multiply <$> mw <*> mx

I would love to be able to use operators to make this a little more elegant in C#, but operators can't be parametrically polymorphic and so the only way is to use this fluent style.

If you have functions with even more arguments then you can simply chain more calls to Apply and it will just work.

Now lets do the applicative-version of the imperative nullable-expression from earlier:

var lhs = multiply.Map(mw).Apply(mx);
var rhs = multiply.Map(my).Apply(mz);
var res = add.Map(lhs).Apply(rhs);

It is more concise than the imperative version, it's less error prone, and it supports every single applicative type ever written. So, we can run this with Either, Option, Seq, etc.

It's not quite as easy to read which is definitely the downside to using applicatives in C#. Most applicatives are also monads and monads (in C#) are 'LINQ friendly'. Which means we could have just written:

var res = from w in mw
          from x in mx
          from y in my
          from z in mz
          select w * x + y * z;

It's probably easier to read and doesn't need any special currying of functions. So, what is it that applicatives have over monads? Namely, monads are about sequential operations – we can only get each operand of the final expression in-sequence, first the w, then the x, then the y, then the z, then we return the result (if all succeeded). If any fail we return immediately and don't process the rest.

Applicatives however do not have sequential processing semantics. In fact, they're the opposite.

Let's take a look at the earlier mathematical expression in tree form. We can see that there are two main branches that are entirely independent of each other. We could calculate the left-hand-side in-parallel to the processing of the right-hand-side before applying the values to the addition function.

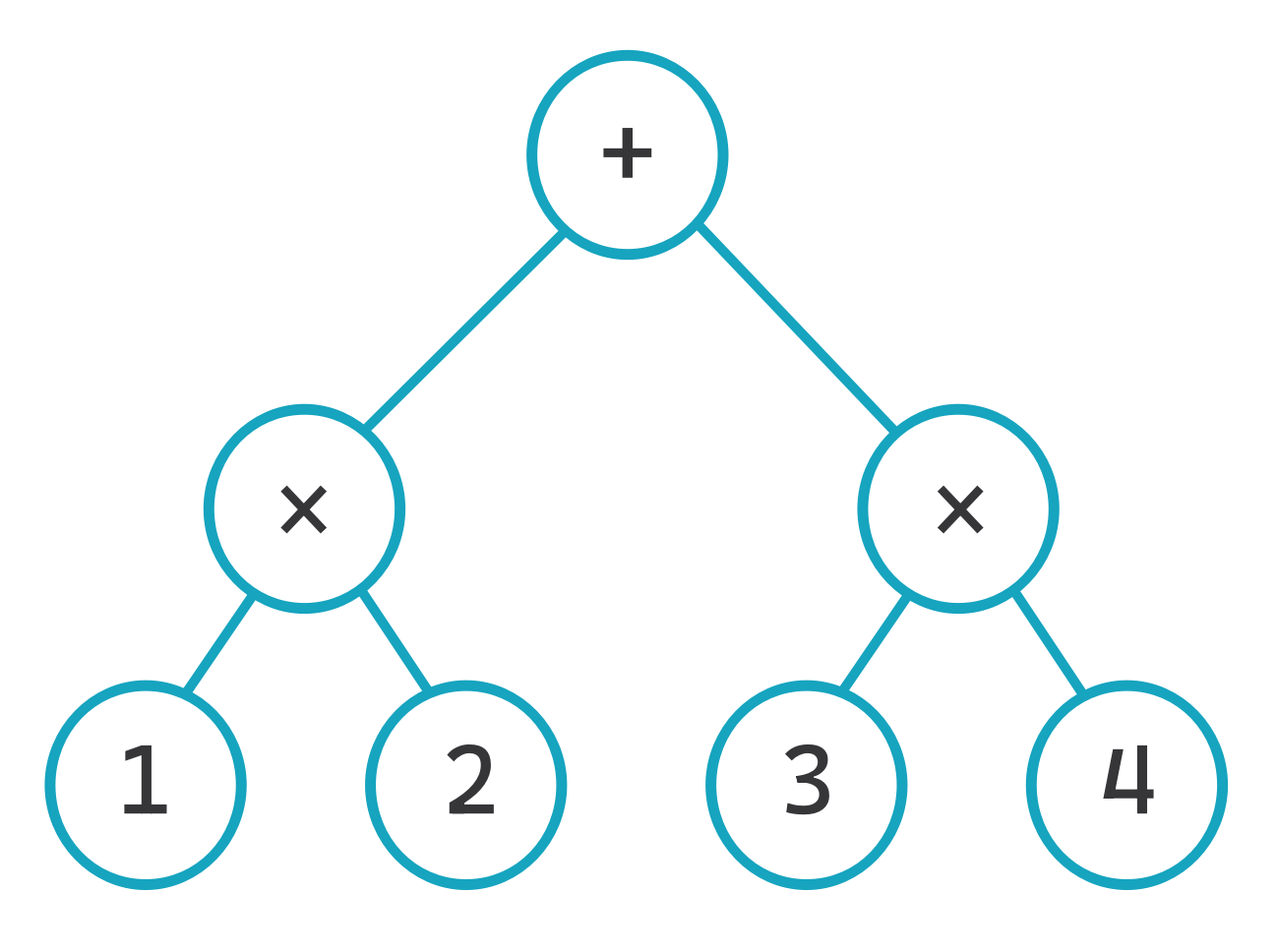
Because applicatives get access to both their function and its argument at the same time, they're able to follow a strategy where the operands are calculated independently.

You can see this in the Apply implementation for IO effect type:

public static IO<B> Apply<A, B>(this IO<Func<A, B>> ff, IO<A> fa) =>
    from tf in ff.Fork()
    from ta in fa.Fork()
    from f in tf.Await
    from a in ta.Await
    select f(a);

Notice how it forks both the function IO and the argument IO. That means they can run in parallel whilst further down the expression awaits both IO operations to complete. If you use functions with more arguments (and therefore chain more Apply calls) then each argument runs in parallel and the final function invocation only occurs when all arguments have been acquired.

And so, applicatives enable automatic parallelisation of effectful computations. No need to manually write code to do threaded coordination.

Here's a simple example. Let's first get three asynchronous IO operations:

var io1 = liftIO(() => File.ReadAllTextAsync(path1));
var io2 = liftIO(() => File.ReadAllTextAsync(path2));
var io3 = liftIO(() => File.ReadAllTextAsync(path3));

And some function that wants to use the result of those operations:

var concat = (string txt1, string txt2, string txt3) =>
                   txt1 + txt2 + txt3;

Next we map and apply the IO computations. These three IO operations will now all run in parallel and collect their results before invoking the concat function.

IO<string> res = concat.Map(io1).Apply(io2).Apply(io3);

You might be thinking "but, you didn't curry the concat function first!". You're right, because language-ext has Map and Apply overrides that will deal with that automatically for multi-argument delegates. The overrides simply curry the function for you before invoking the regular Map and Apply methods.

Another thing to note with the above expression is that Map is called on the function – and so it doesn't get forked; only io1, io2, and io3 get forked. That means we're not launching pointless parallel processes to acquire the function (which would normally be available already).

Applicatives are a little hard to get your head around at first – but they are incredibly powerful. Even if you don't need the more 'hierarchal' behaviour (as opposed to the sequential behaviour of monads) they can – in the right circumstance – be very concise and elegant. However, in C# it isn't always the case, so it's best to pick your battles and use them when you need their unique capabilities or when the resulting code will be more elegant.

This article is a little long now – I still haven't explained the Pure method in Applicative and I wanted to cover how applicatives can be used for validation – but I think I'll dedicate a separate article to that so I can give some more real-world examples.

Part 5 – Validation

Subscribe

This site is an independent publication launched in February 2024 by Paul Louth. If you subscribe today, you'll get full access to the website as well as email newsletters about new content when it's available. Your subscription makes this site continue to exist. Thank you!

Fresh content, delivered

Stay up to date with new content sent straight to your inbox! No more worrying about whether you missed something because of a pesky algorithm or news feed.