Higher Kinds in C# with language-ext [Part 5 - validation]
![Higher Kinds in C# with language-ext [Part 5 - validation]](/content/images/size/w960/2024/03/Validation-1.png)
This is a multi-part series of articles, it's worth going back to the earlier parts if you haven't read them already:
- Part 1 - Introduction, traits, semigroups, and monoids
- Part 2 - Functors
- Part 3 - Foldables
- Part 4 - Applicatives
NOTE: For those lovely people who have subscribed and are wondering "Where's the newsletter?" – I am sorry, unfortunately this platform (GhostCMS) insists on using Mailgun to do mass mailing and has no other options. After trying Mailgun I have never been so offended by a SaaS service in my life – it is awful. So, I will write my own that sends via Sendgrid, or something like that, eventually. My current focus has been trying to get language-ext to beta ASAP and so I will look at the newsletter sending when I have a bit of free time!
In the last article I introduced the Applicative trait and showed how it can be used to perform operations on 'lifted' values. The benefit of working in the 'lifted' environment is that we don't have to unpack the values, perform the operation, and then repack the values manually – the applicative functor does that for us. It is the same with Functor – we don't have to manually pattern-match the Maybe type, the Either type, or iterate the values in the List type — the functor does that job for us. These techniques are boilerplate removers!
But, where does the 'lifted' vernacular come from?
Take a look at Diagram 1 below. At the bottom of the diagram is a blue arrow linking A to B (which I will write A → B). The label f represents a single argument function that takes any value of type A and returns a value of type B – it's a Func<A, B>.
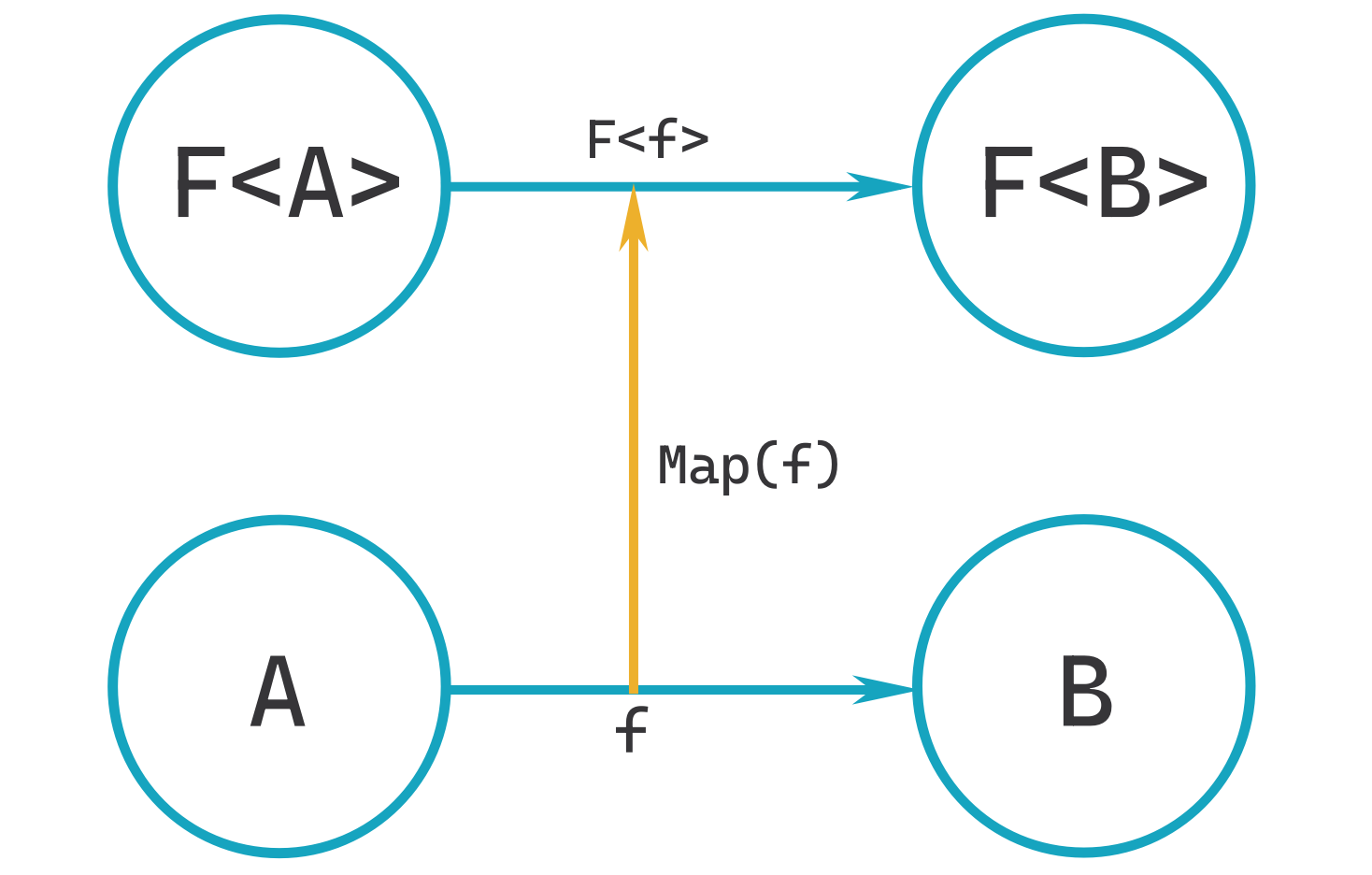
At the top of the diagram is an equivalent of A → B but with an outer F wrapping. This is the applicative-functor F. With functor F we can map F<A> to F<B> using the function F<f> – which is F<Func<A, B>>.
If you remember from, the last article, the Apply function looks like this:
K<F, B> Apply<A, B>(K<F, Func<A, B>> mf, K<F, A> ma)It should be fairly obvious that we can project K<F, A> → K<F, B> using K<F, Func<A, B>> – which maps to the top section of the diagram above. What we're doing when we Apply is to do the equivalent of f.Invoke(a) where f is a regular delegate; but we're invoking for something with additional structure (Maybe, List, Either, ...). So, Apply is just Invoke for lifted structures.
Again, 'lifted', why lifted? Well, the etymology isn't entirely clear, but I believe that it's simply because when drawn out in diagram form (as above), the lifted elements are literally above the others. It is also the origin of 'higher' in higher-kinds.
It's fascinating that none of the Wikipedia references for lifting – whether it's category-theory or functional-programming related – specifies the etymology. If you have a reference to the etymology, or a better understanding of its mathematical origins, I'd be very interested to see it!
Even if my definition isn't the true etymology, this is how I like to think of it. We lift simple values and functions into a 'higher space'. And we try, as much as possible, to work in that higher-space; only coming back down when we have a concrete and robust way of doing so. For example, if you have a Maybe<string> – only come back down to string when you have a meaningful default for the Nothing case. Otherwise, continue the optional computation in its higher-space using Map, Apply, etc.
The orange/vertical arrow in Diagram 1 is the process of lifting in action. The Map function in Functor lifts a – 'lower' – Func<A, B> function and makes it into a 'higher' lifted function that can be applied to values of F<A>. You can think of Map as both the operation to lift the function and the application of the argument (Apply). Whereas Apply will only work with pre-lifted functions.
If we put some real types in there then it becomes a little less abstract and slightly more obvious what's really going on.
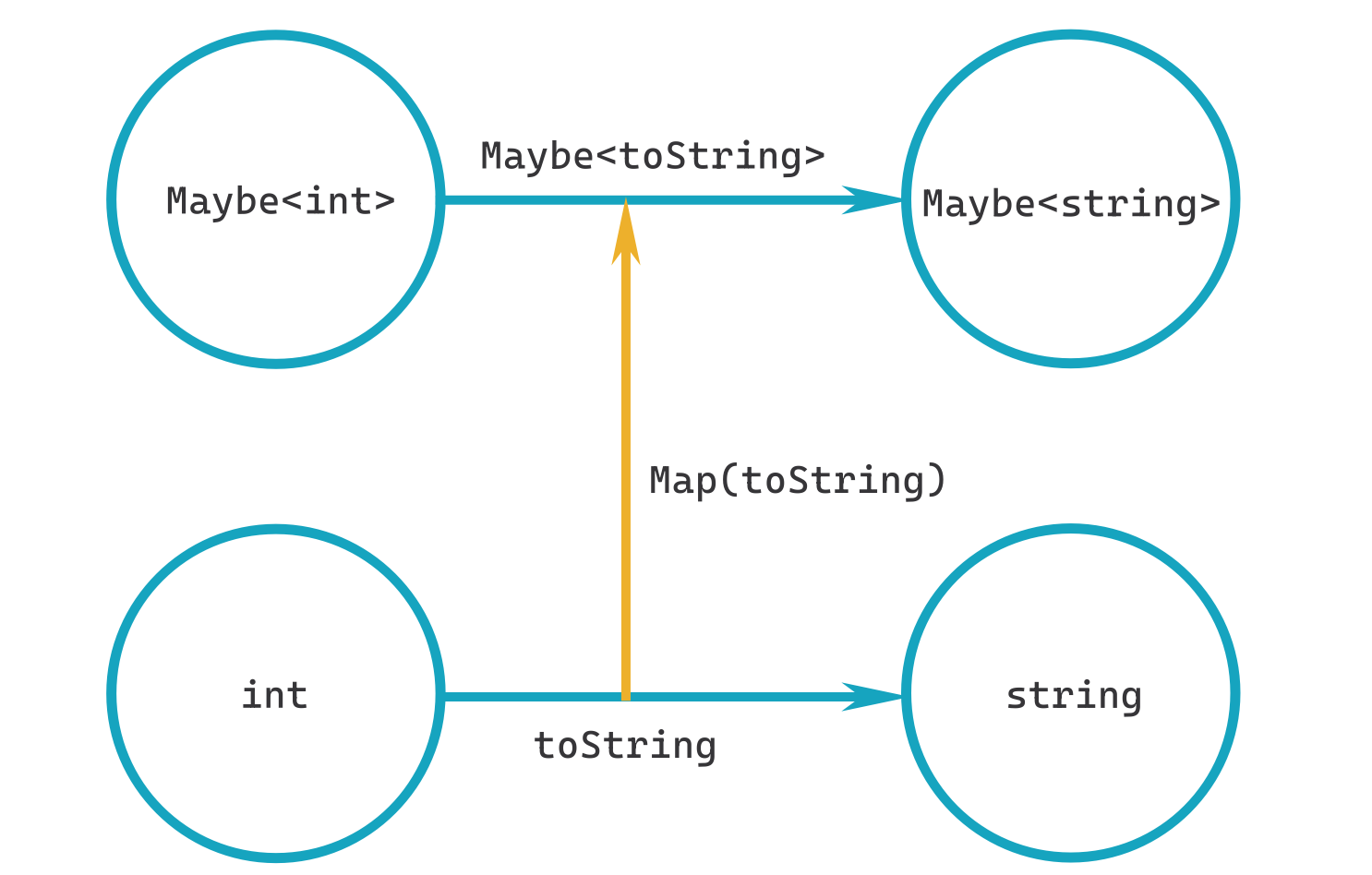
There seems to be a couple of arrows missing from the diagram however. If we can lift a function from being just a function to being an embellished function. Can we do the same with int → Maybe<int> and string → Maybe<string>?
Yes, we can:
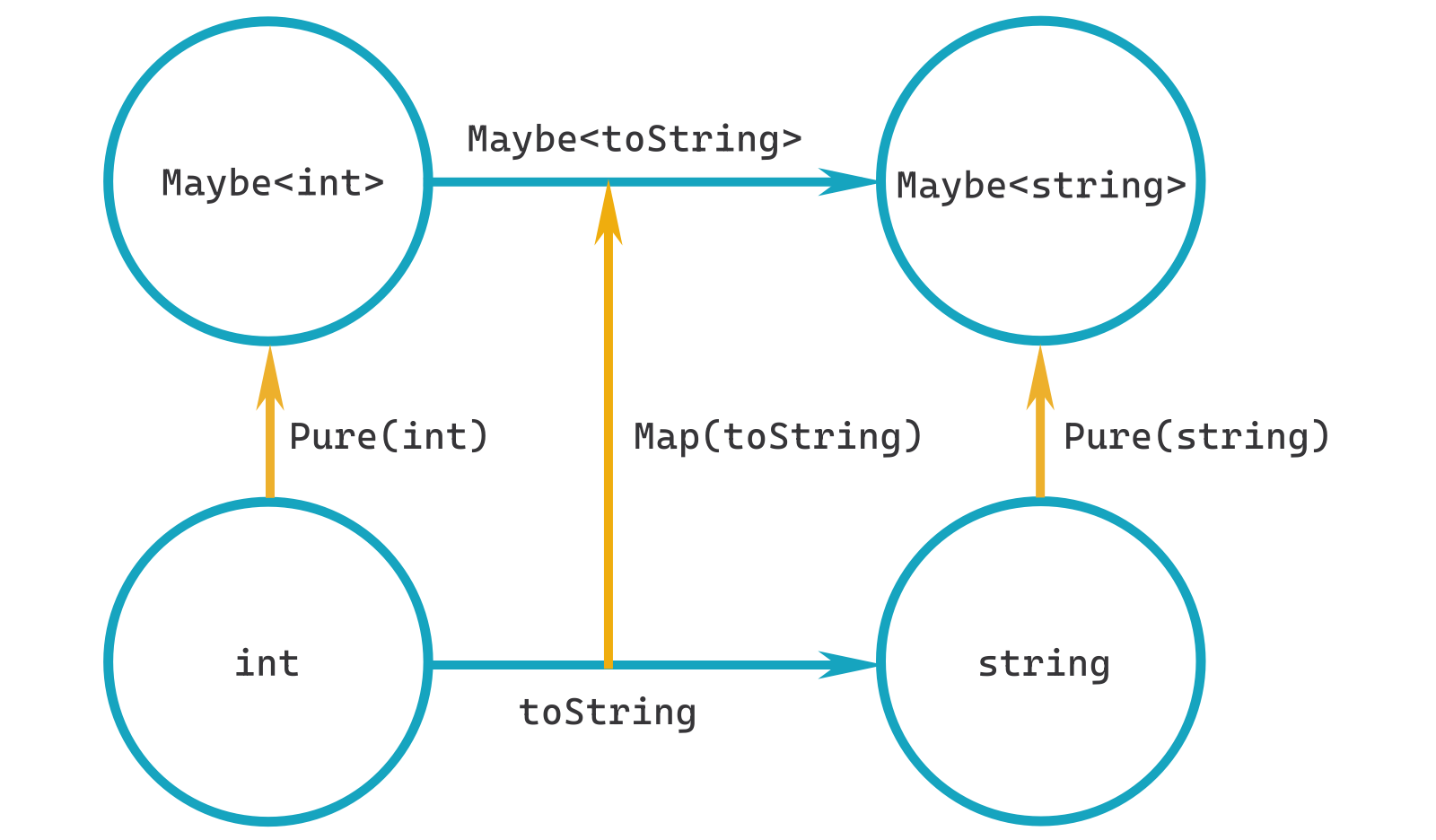
The two new arrows are gained from the Pure function that's part of the Applicative trait. So, with Pure and Map we are able to lift anything we want from being a regular value or function and make them into embellished values and functions.
I'm saying 'embellished' to mean 'giving extra capabilities to'. So,Maybe<int>is anintwith an optionality embellishment!
In diagram form functors and applicative-functors become quite tame – there isn't any great mystery behind them, they're simply mechanisms that allow us to continue working in a lifted space. This drawing of arrows between types is the essence of Category Theory and is much simpler than the name sounds.
So, now that I've explained the complete interface for Applicative, let's look at another concrete usage of applicatives: Validation.
Validation is definitely part of the 'awkward squad', it's never trivial to build validation into any application. It always seems trivial on the surface, but doing it well, isn't.
Let's try and validate a credit-card and associated details using the language-ext built-in Validation type. Then we can dissect how and why it works...
First, let's create the data model for what we expect the result of validating a credit-card to be:
// Credit care number
public record CardNumber(Seq<int> Number);
// Expiry date
public record Expiry(int Month, int Year);
// CVV code
public record CVV(int Number);
// Complete credit card details
public record CreditCardDetails(CardNumber CardNumber, Expiry Expiry, CVV CVV)
{
public static CreditCardDetails Make(CardNumber cardNo, Expiry expiry, CVV cvv) =>
new (cardNo, expiry, cvv);
}
I realise these are declared as records and therefore we can't control their construction; but it reduces the amount of code I need to write here! You might want to protect their construction with classes instead.
We have a card-number which holds the 16 digit credit-card number, an expiry-date in Month/Year format, a 3 digit CVV number, and a composition of all of those types, making CreditCardDetails. Pretty simple.
Let's start with the simplest item, the CVV number. The rules are:
- Must be all digits
- Must be 3 digits in length
Part of the power of writing pure functional code is its powerful composition. Meaning we can build complex things from simple things. So, let's start with some simple things:
static Validation<Error, int> CharToDigit(char ch) =>
ch is >= '0' and <= '9'
? Pure(ch - '0')
: Fail(Error.New($"expected a digit, but got: {ch}"));
Ok, so we take a char, check that it's one of the digit characters and if so, we return Pure(ch - '0') – Pure should have meaning to you now as the function that lifts values.
Because this is C# and C#'s type inference is awful,Pureactually constructs the typePure<A>. This can be seen as an intermediate value until the type-system has enough information to infer. At the point of construction the functionPure(...)knows nothing aboutError, meaning we'd have to specify it. However, later, an implicit conversion can happen fromPure<int>toValidation<Error, int>and we don't need to specify theErrortype.
If the value isn't a digit, then we call Fail – which works a bit like Pure but for failure values. It constructs the type Fail<E> (where E is the error-type).
There are some circumstances where, even with this technique, Pure and Fail don't resolve – and so the alternative is to directly construct the Validation value you need. For example:
static Validation<Error, int> CharToDigit(char ch) =>
ch is >= '0' and <= '9'
? Validation<Error, int>.Success(ch - '0')
: Validation<Error, int>.Fail(Error.New($"expected a digit, but got: {ch}"));Hopefully it's clear why Pure and Fail are so useful. It's much more elegant. All of the core types in language-ext support implicit conversion from Pure and Fail (and have SelectMany overrides so they can work in LINQ expressions also).
Anyway, back to the validation! We have a simple function that validates whether a char is a digit and, if so, it converts it to an int – otherwise it fails with a useful error message.
If we try it out:
CharToDigit('x');
CharToDigit('1');We will get this output:
Fail(expected a digit, but got: x)
Success(1)Which is exactly what we want!
The CVV code is multiple digits though; so let's start leveraging the power of pure functional composition to check that all of the characters are digits:
static Validation<Error, EnumerableM<int>> ValidateAllDigits(string value) =>
value.AsEnumerableM()
.Traverse(CharToDigit)
.As();
This converts the string to an EnumerableM, traverses each item, running the conversion.
EnumerableMis a simple wrapper-type forIEnumerable– it supports:Functor,Foldable,Traversable,Applicative,Monad,SemigroupK, andMonoidK– so it's likeIEnumerableon steroids!
Let's try ValidateAllDigits :
ValidateAllDigits("xy123");
ValidateAllDigits("123");This outputs:
Fail([expected a digit, but got: x, expected a digit, but got: y])
Success([1, 2, 3])Notice how we get two errors returned for "xy123" – it is picking up both x and y as invalid digit characters and informing us of both issues.
This automatic tracking of multiple errors is enabled by the applicative capability of the Validation type. We'll dissect that later.Now that we can prove all the of the characters in the string are digits, we can provide a wrapper function that maps the value to an int.
static Validation<Error, int> ValidateInt(string value) =>
ValidateAllDigits(value).Map(_ => int.Parse(value));
We don't bake this into the ValidateAllDigits function, because when we test the card-number later we won't convert it to an int. This gives us two functions that validate, one of which maps the value.
I won't test this, because it's obvious it will work!
Ok, so we can now test that the CVV is a multidigit value, but we haven't asserted that it's exactly three digits in length. Just to show off, let's do length validation for any foldable:
static Validation<Error, K<F, A>> ValidateLength<F, A>(K<F, A> fa, int length)
where F : Foldable<F> =>
fa.Count() == length
? Pure(fa)
: Fail(Error.New($"expected length to be {length}, but got: {fa.Count()}"));
This leverages the built-in Count() extension for foldables.
But, because string isn't a foldable, let's create a version that turns the string into a foldable so it can be validated:
static Validation<Error, string> ValidateLength(string value, int length) =>
ValidateLength(value.AsEnumerableM(), length)
.Map(_ => value);
This is obviously overkill, but whatever, we're enjoying ourselves!
Time to test it:
ValidateLength("xy123", 3);
ValidateLength("123", 3);Which outputs:
Fail(expected length to be 3, but got: 5)
Success(123)
Hopefully, you're also starting to see how easy this stuff is to test. These components are all pure and have no external moving parts – making testing trivial.
So, now we have the components to assert our spec for the CVV code:
- Must be all digits
- Must be 3 digits in length
Let's compose them together:
static Validation<Error, CVV> ValidateCVV(string cvv) =>
fun<int, string, CVV>((code, _) => new CVV(code))
.Map(ValidateInt(cvv))
.Apply(ValidateLength(cvv, 3))
.As();Here we start to see the standard applicative pattern start to emerge: a chain of Map follow by Apply – it's something that becomes very familiar after a while.
Let's try it out:
ValidateCVV("xy123");
ValidateCVV("123");
It outputs:
Fail([expected a digit, but got: x, expected a digit, but got: y, expected length to be 3, but got: 5])
Success(123)
We're collecting all of the errors! It's really starting to look more like the kind of output you'd see from a compiler. This is really powerful stuff.
This is all using the built-in Error type. A more advanced solution to this would be to create a bespoke error type that captures context better than raw text messages. For example, the errors could all be grouped together and displayed much better than repeating the same "expected a ..." text.Now we have the CVV validator, let's look at the expiry date. Our rules will be:
- Must be in the format
<MM>['\' | '/' | '-' | ' ']<YYYY>– some examples:12-202401/202506 2029
- The first part (the month) must be an integer from
1 – 12 - The second part must be:
- A four digit integer
- Equal to this year or a year in the next 10
We already have the ValidateInt function from earlier, we can re-use that. The next thing we're going to need is to check whether the parts of the date (the month and the year) are in range. The range is from now to ten years in the future. Dates are a little tricky, so instead of making the validator too complex, let's extend the Expiry type to act like a complex number that we can do range based operations on:
// Expiry date
public record Expiry(int Month, int Year) :
IAdditionOperators<Expiry, Expiry, Expiry>,
IComparisonOperators<Expiry, Expiry, bool>
{
public static readonly Expiry OneMonth = new (1, 0);
public static Expiry operator +(Expiry left, Expiry right)
{
var m = left.Month + right.Month;
var y = left.Year + right.Year;
while (m > 12)
{
m -= 12;
y++;
}
return new Expiry(m, y);
}
public static bool operator >(Expiry left, Expiry right) =>
left.Year > right.Year ||
left.Year == right.Year && left.Month > right.Month;
public static bool operator >=(Expiry left, Expiry right) =>
left.Year > right.Year ||
left.Year == right.Year && left.Month >= right.Month;
public static bool operator <(Expiry left, Expiry right) =>
left.Year < right.Year ||
left.Year == right.Year && left.Month < right.Month;
public static bool operator <=(Expiry left, Expiry right) =>
left.Year < right.Year ||
left.Year == right.Year && left.Month <= right.Month;
public static Expiry Now
{
get
{
var now = DateTime.Now;
return new Expiry(now.Month, now.Year);
}
}
public static Range<Expiry> NextTenYears =>
LanguageExt.Range.fromMinMax(Now, Now + new Expiry(0, 10), new Expiry(1, 0));
}I won't go into too much detail on that because it's pretty regular C#. But, the things to note are that it now supports the addition operator that understands how to add months and years. And it can do comparisons that take into account the month and year correctly. Finally, it exposes a language-ext Range that is from Now to 10 years from now.
That NextTenYears range is what we will validate against...
Let's create a general range validator:
static Validation<Error, A> ValidateInRange<A>(A value, Range<A> range)
where A : IAdditionOperators<A, A, A>,
IComparisonOperators<A, A, bool> =>
range.InRange(value)
? Pure(value)
: Fail(Error.New($"expected value in range of {range.From} to {range.To}, but got: {value}"));
It takes a value and a range and tests if the value is within the range. Let's test it:
ValidateInRange(new Expiry(10, 2024), Expiry.NextTenYears);
ValidateInRange(new Expiry(2, 2034), Expiry.NextTenYears);
ValidateInRange(new Expiry(10, 2034), Expiry.NextTenYears);
ValidateInRange(new Expiry(1, 2023), Expiry.NextTenYears);It outputs:
Success(10/2024)
Success(2/2034)
Fail(expected value in range of 3/2024 to 3/2034, but got: 10/2034)
Fail(expected value in range of 3/2024 to 3/2034, but got: 1/2023)Nice! It's always better if you can make a complex pairing like month and year work together in a single value-type. Of course we could have leveraged DateTime but this is more precise and declarative.
Now let's compose that into something that validates a month and a year string:
static Validation<Error, Expiry> ValidateExpiryDate(string expiryDate) =>
expiryDate.Split(['\\', '/', '-', ' ']) switch
{
[var month, var year] =>
from my in ValidateInt(month) & ValidateInt(year)
let exp = new Expiry(my[0], my[1])
from _ in ValidateInRange(exp, Expiry.NextTenYears)
select exp,
_ => Fail(Error.New($"expected expiry-date in the format: MM/YYYY, but got: {expiryDate}"))
};This is a little bit harder to parse. First we spit the expiryDate string. We are expecting two parts, so we pattern match to extract the month and year parts. If the match fails then we yield an explanatory error.
We then call ValidateInt twice. One for month and one for year. They are composed using the & operator. When you find that all terms of an Apply expression yield the same type then you can use & or | to check for any errors. & will collect the results of the operands into a Seq (if all are successful), whereas | will continue if either operand is successful, but if both fail then it will collect all of the errors.
NOTE: The|operator works slightly differently inv5compared tov4.v4was closer to the&behaviour. So, when migrating it is worth finding all usages ofValidationand migrating|to&.
That means my is a Seq<int> if both the month and the year validate as integers. We can then create a new Expiry and check that the expiry date is within the valid range.
Let's test...
ValidateExpiryDate("10-2024");
ValidateExpiryDate("02-2034");
ValidateExpiryDate("10/2034");
ValidateExpiryDate("1/2023");
ValidateExpiryDate("1X2023");
ValidateExpiryDate("02-F00");
It outputs:
Success(10/2024)
Success(2/2034)
Fail(expected value in range of 3/2024 to 3/2034, but got: 10/2034)
Fail(expected value in range of 3/2024 to 3/2034, but got: 1/2023)
Fail(expected expiry-date in the format: MM/YYYY, but got: 1X2023)
Fail(expected a digit, but got: F)Yeah, this is good! Meaningful validation output.
Now we need to validate the main credit-card number, here's the final function:
static Validation<Error, CardNumber> ValidateCardNumber(string cardNo) =>
(ValidateAllDigits(cardNo), ValidateLength(cardNo, 16))
.Apply((digits, _) => digits.ToSeq())
.Bind(ValidateLuhn)
.Map(digits => new CardNumber(digits))
.As();We've already seen the ValidateAllDigits and the ValidateLength validators, what we haven't seen is Apply used on a tuple of Validation types. This is an alternatives approach to calling Apply – for some circumstances it's more elegant as you don't need to provide the type-signature of the lambda.
NOTE: Sometimes the tuple-basedApplydoesn't pass the C# type-checker. TheApplymethods extend(K<F, A>, F<F, B>, ...)and it seems sometimes C# doesn't want to coerce the value to its underlying interface – I'm not sure the exact rules around this, I will dig some more, but if you face this problem you can just chain theMapandApplyfunctions as seen in the examples up to now.
ValidateLuhn is also called sequentially using the monadic Bind operation. We'll discuss monads in a later article – but just know that Bind operation runs after we've validated that the card-number is 16-digits in length.
What about ValidateLuhn – what does it do? Let's look at it:
static Validation<Error, Seq<int>> ValidateLuhn(Seq<int> digits)
{
int checkDigit = 0;
for (int i = digits.Length - 2; i >= 0; --i)
{
checkDigit += ((i & 1) is 0) switch
{
true => digits[i] > 4 ? digits[i] * 2 - 9 : digits[i] * 2,
false => digits[i]
};
}
return (10 - checkDigit % 10) % 10 == digits.Last
? Pure(digits)
: Fail(Error.New("invalid card number"));
}This is an implementation of the Luhn algorithm, which is essentially a check-sum for credit-card numbers. It makes sure the person who typed it in didn't make a mistake. I haven't modified it much from the version on the Wikipedia page, I've simply made it accept a Seq<int> and return a Validation depending on whether the check-sum succeeds or not. So, I won't dwell on this implementation too much.
It does however mean that ValidateCardNumber should check that each character is a digit, that the length of the digits is 16 characters, and that the digits pass the Luhn algorithm check-sum. Let's try it:
ValidateCardNumber("4560005094752584");
ValidateCardNumber("00000");
ValidateCardNumber("000000000000000x");
ValidateCardNumber("0000000000000000x");It outputs:
Success([4, 5, 6, 0, 0, 0, 5, 0, 9, 4, 7, 5, 2, 5, 8, 4])
Fail(expected length to be 16, but got: 5)
Fail(expected a digit, but got: x)
Fail([expected a digit, but got: x, expected length to be 16, but got: 17])The credit card number is a fake btw!
So, we have all of the component parts now. We should be able to do the final validator:
public static Validation<Error, CreditCardDetails> Validate(string cardNo, string expiryDate, string cvv) =>
fun<CardNumber, Expiry, CVV, CreditCardDetails>(CreditCardDetails.Make)
.Map(ValidateCardNumber(cardNo))
.Apply(ValidateExpiryDate(expiryDate))
.Apply(ValidateCVV(cvv))
.As();
Here we get to see the pure functional composition really starting to open up. I really love seeing this stuff. We have combined small components (like digit-validators, integer-validators, range-validators, etc. into larger components, like ValidateCardNumber, ValidateExpiryDate, and ValidateCVV. And now, we get to compose those bigger components into an even bigger component.
It's pure all the way down! It's robust and error free all the way down! It's turtles all the way down! These things stick together like Lego – once you've built your core components then they all stack up beautifully.
Let's do the final test:
Validate("4560005094752584", "12-2024", "123");
Validate("00000", "00-2345", "XYZ");
It outputs:
Success(CreditCard([4, 5, 6, 0, 0, 0, 5, 0, 9, 4, 7, 5, 2, 5, 8, 4], 12/2024, 123))
Fail([expected length to be 16, but got: 5, expected value in range of 3/2024 to 3/2034, but got: 0/2345, expected a digit, but got: W, expected a digit, but got: X, expected a digit, but got: Y, expected a digit, but got: Z])
That all works exactly as it should, we have lots of errors that show at a fine-grained level what the issues were with the credit-card details. The thing is, maybe it's too fine-grained? Do we really care about individual digits being letters? Are the error messages descriptive enough? I'd say "no". We can do better.
When we're parsing a char to see if it's a digit we have no idea that it's part of a CVV code or card-number, so we can't give context. But we can add that context higher up the stack: This is where MapFail comes in. It allows you to take an error and provide more context higher up the stack where you have it.
Here's a version of ValidateCVV which overrides the simpler errors messages and provides something contextual:
static Validation<Error, CVV> ValidateCVV(string cvv) =>
fun<int, string, CVV>((code, _) => new CVV(code))
.Map(ValidateInt(cvv).MapFail(_ => Error.New("CVV code should be a number")))
.Apply(ValidateLength(cvv, 3).MapFail(_ => Error.New("CVV code should be 3 digits in length")))
.As();
You could do other things like create Error hierarchies where the inner-errors hold the more fine-grained errors and they're wrapped in a more contextual error. This can be great for debugging purposes – where you want to carry the raw info but also give friendly errors to end-users.
For example, if we take the ValidateCardNumber from earlier and use MapFail:
static Validation<Error, CardNumber> ValidateCardNumber(string cardNo) =>
(ValidateAllDigits(cardNo), ValidateLength(cardNo, 16))
.Apply((digits, _) => digits.ToSeq())
.Bind(ValidateLuhn)
.Map(digits => new CardNumber(digits))
.As()
.MapFail(e => Error.New("card number not valid", e)); The final MapFail there will capture any failure and wrap it up in a new error that simply has the message "card number not valid" – but it carries the details in its Inner property.
If we run the test from before with these new changes:
Validate("00000", "00-2345", "WXYZ")We get:
Fail([card number not valid, expected value in range of 3/2024 to 3/2034, but got: 0/2345, CVV code should be a number, CVV code should be 3 digits in length])So now we have 4 errors, each explaining clearly what the problem is, but there is also some inner errors that give even more context if needed. Nice!
All of this behaviour is enabled by applicatives. If you remember from the last article the IO monad was able to run things in parallel (in its Apply function). It was leveraging the fact that it could wait for the successful result of two operations before applying the values. Validation works the opposite way, it waits for the failure results of two operations and combines them.
Here is the Apply trait implementation for Validation:
static K<Validation<FAIL>, B> Applicative<Validation<FAIL>>.Apply<A, B>(
K<Validation<FAIL>, Func<A, B>> mf,
K<Validation<FAIL>, A> ma) =>
mf switch
{
Validation.Success<FAIL, Func<A, B>> (var f) =>
ma switch
{
Validation.Success<FAIL, A> (var a) =>
Validation<FAIL, B>.Success(f(a)),
Validation.Fail<FAIL, A> (var e) =>
Validation<FAIL, B>.Fail(e),
_ =>
Validation<FAIL, B>.Fail(FAIL.Empty)
},
Validation.Fail<FAIL, Func<A, B>> (var e1) =>
ma switch
{
Validation.Fail<FAIL, A> (var e2) =>
Validation<FAIL, B>.Fail(e1 + e2),
_ =>
Validation<FAIL, B>.Fail(e1)
},
_ => Validation<FAIL, B>.Fail(FAIL.Empty)
};If you follow the pattern-match through the two Validation.Fail cases, you'll see it calls e1 + e2 which are the two error values being combined into one.
The other thing to note is that Validation can have any value for its FAIL case as long as it's a Monoid (go back to the first article in this series for a reminder about monoids). So, if you want to implement a bespoke error type then make sure you make it monoidal.
Ok, so this article definitely went on longer than I expected! I did feel it was important to really see the benefits of the applicative-functor approach though – because I think it's a trait that gets overlooked quite often – mostly because it's not as pretty as functors and monads, but the compositional power of applicatives should not be ignored!
Because there's a lot of code in this article I've uploaded it all to a gist for your convenience.
Next up, traversables...
Subscribe
This site is an independent publication launched in February 2024 by Paul Louth. If you subscribe today, you'll get full access to the website as well as email newsletters about new content when it's available. Your subscription makes this site continue to exist. Thank you!
Fresh content, delivered
Stay up to date with new content sent straight to your inbox! No more worrying about whether you missed something because of a pesky algorithm or news feed.