Higher Kinds in C# with language-ext [Part 6 - traversables]

This is a multi-part series of articles, it's worth going back to the earlier parts if you haven't read them already:

• Part 1 - Introduction, traits, semigroups, and monoids
• Part 2 - Functors
• Part 3 - Foldables
• Part 4 - Applicatives
• Part 5 - Validation

NOTE: For those lovely people who have subscribed and are wondering "Where's the newsletter?" – I am sorry, unfortunately this platform (GhostCMS) insists on using Mailgun to do mass mailing and has no other options. After trying Mailgun I have never been so offended by a SaaS service in my life – it is awful. So, I will write my own that sends via Sendgrid, or something like that, eventually. My current focus has been trying to get language-ext to beta ASAP and so I will look at the newsletter sending when I have a bit of free time!

One interesting stat is that I have managed to remove nearly half a million lines of code from the v5 release of language-ext. At least 200,000 of those lines were auto-generated by some T4 templates (LanguageExt.Transfomers, which has now been deleted entirely); the rest of the deletions were from hand-written types and extension methods used to simulate higher-kinds (OptionAsync<A> for example, is emulating the (new) monad-transformer stack OptionT<IO, A>).

The reason that so many lines of code have been removed is because we don't need to emulate higher-kinds any more, we really can write: OptionT<IO, A> (I'll talk about transformers in a later article). So, if the removal of nearly half a million lines of code doesn't justify the techniques I am highlighting in this series, I really don't know what will! Less code pretty much always means fewer bugs and easier long-term maintenance – something I am particularly looking forward to once this release is stable!

Also, remember, that v5 has much more functionality – not less!

One thing I noticed as I was working through all of the original language-ext unit-tests – trying to turn them all green – was that I discovered some tests-cases where both the code and the unit-test had a bug. The bugs discovered were in the manually written Traverse and Sequence functions.

On [some of the implementations of Traverse] I had made wrong assumptions and I had carried those wrong assumptions through to the unit-tests! It doesn't matter how good you are at programming, you will always end up making stupid mistakes like this – which is why I much prefer to leverage types over unit-tests: you can't cheat the compiler, but you can easily cheat yourself!

The new implementations of Traverse (leveraging the higher-kinded traits) exposed those bugs – because they are now following the rules of the trait-types – not the assumptions of a human that errs.

In the Foldables article I showed the graph from the Haskell Typeclassopedia – we're quite a way into implementing the key traits from this diagram:

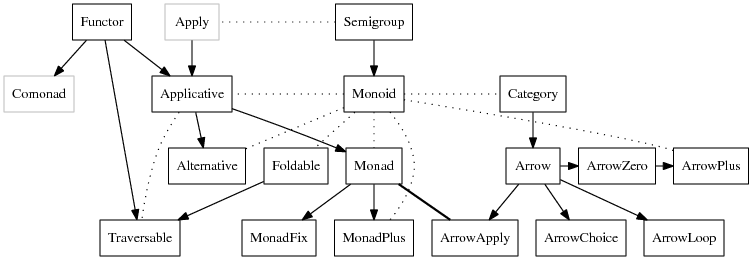
In this article we will take on the Traversable trait. You can see from the diagram above that there are three arrows leading into the Traversable trait: Functor, Foldable, and Applicative. We have already implemented these in previous articles, so we have all of the components needed to create a Traversable trait.

But what are traversables? Simply, traversables are a little bit like foldables in that you can iterate over many items in a structure, aggregating as you go. Except, traversables don't expose an aggregated state-value, they instead return a nested foldable/applicative structure. The aggregation comes from running the default applicative behaviour for the structure instead of a provided fold function. This nested structure is 'flipped' so what was inner becomes outer and what was outer becomes inner.

That explanation is too abstract, so let's take a look at an example. Below, we have a collection of strings that we want to parse into integers. Not all strings can be parsed into a valid integer, so we need a way to deal with the failure to parse:

var items = Seq("1", "2", "3", "4", "5");
var values = items.Map(s => parseInt(s));

The example above takes a Seq<string>, each value is passed to the parseInt function from the language-ext Prelude. parseInt returns an Option<int>. And so, the result of this would be:

[Some(1), Some(2), Some(3), Some(4), Some(5)]

So, the success of the parsing is embedded into the list.

If we had an item that caused a failure:

var items = Seq("1", "2", "3", "X", "5");  // NOTE: 4th item is 'X'
var values = items2.Map(s => parseInt(s));

Then the result looks like this:

[Some(1), Some(2), Some(3), None, Some(5)]

Now we can tell which items succeed and which failed. Which on its own is pretty useful, but if we want to work with the values in the list we have to do work on every step to test that the value exists.

Often, we want to know whether all items succeeded and only proceed if that is the case. And we often want to early out if any fail, not to continue to parse the rest of the list.

This is where Traverse comes in. Simply replace Map with Traverse:

var items = Seq("1", "2", "3", "4", "5");
var values = items.Traverse(s => parseInt(s));

Now the output is this:

Some([1, 2, 3, 4, 5])

We have 'flipped' the type. Instead of a Seq<Option<int>> we now have an Option<Seq<int>> – this is the magic of traverse. It follows the rules of the outer applicative (Option) to accumulate the inner foldable (Seq) – resulting in the behaviour of Option being embedded for each item in the sequence.

If we have a collection where the transformation would produce None ...

var items = Seq("1", "2", "3", "X", "5");
var values = items.Traverse(s => parseInt(s));

... then we get:

None    // Option<Seq<int>>

If any item fails, they all fail.

This works for all foldables with all applicatives – injecting the default applicative behaviour for each step (which, by the way, may not shortcut the operation, as it does with Option).

Here's a simple example using the generic IO library with the Eff monad:

var items = Seq("c:\\test1.txt", "c:\\test2.txt", "c:\\test3.txt");
var values = items.Traverse(File<Eff<Runtime>, Runtime>.readAllText);

That will read all of the files (in parallel). If any fail then the whole thing fails.

Applicatives such as the Validation type from the last article would collect all of the errors during a Traverse call. And so, it should be clear that there's a lot of power lurking inside these combined types.

It can't be understated how valuable Traverse is for pure functional programming. It is one of the most powerful tools to reach for when you find your types are 'the wrong way around' – that is: the flipping of the types and the injecting of the default applicative behaviour allows for some incredibly concise transformations. As you can see it works especially well with sequences of values – but it's not only for sequences!

Let's look at the trait definition:

public interface Traversable<T> : Functor<T>, Foldable<T> 
    where T : Traversable<T>, Functor<T>, Foldable<T>
{
    public static abstract K<F, K<T, B>> Traverse<F, A, B>(
        Func<A, K<F, B>> f,
        K<T, A> ta)
        where F : Applicative<F>;

    // ... default implementations removed for clarity ...
}

This is enough to hurt anybody's head! I remember when I was first learning Haskell and I saw the type-signature for traverse – it took me quite some time to really grok it. Primarily because I had never really dealt with multiple levels of higher-kinded types before, so it messed with my brain a bit.

Here's the Haskell definition:

class (Functor t, Foldable t) => Traversable t where
    traverse :: Applicative f => (a -> f b) -> t a -> f (t b)

    -- default implementations removed for clarity ...

You should be able to see that we have the same constraints on the class/interface as well as the same constraint on the traverse / Traverse function:

• (Functor t, Foldable t) is the same as : Functor<T>, Foldable<T>
• Applicative f => is the same as where F : Applicative<F>

The traverse / Traverse function also has the same arguments and return type:

• (a -> f b) is the same as Func<A, K<F, B>>
• t a is the same as K<T, A>
• f (t b) is the same as K<F, K<T, B>>

The return type – f (t b) – was what confused me when I was learning Haskell. It should be a little clearer to you seeing the C# version: it's two, nested, higher-kinded types.

We have two higher-kinds: F and T. F is constrained to be an applicative-functor and T is constrained to be a functor and a foldable.

So, we pass in a value that can be folded over and mapped. We also pass in a function that takes the bound-value of the foldable/mappable; it returns the applicative K<F, B>.

So, it should be fairly obvious that we somehow iterate over each value in the foldable/mappable ta, pass each value to the function f, and get a value back for each item. What isn't clear is how that K<F, B> turns into a K<F, K<T, B>>.

As we're calling Traverse on Seq<string> above, let's first look at the implementation of Traverse for the Seq type:

static K<F, K<Seq, B>> Traverse<F, A, B>(Func<A, K<F, B>> f, K<Seq, A> ta) 
{
    return F.Map<Seq<B>, K<Seq, B>>(
        ks => ks, 
        Foldable.foldBack(cons, F.Pure(empty<B>()), ta));

    K<F, Seq<B>> cons(K<F, Seq<B>> xs, A x) =>
        Applicative.lift(Prelude.Cons, f(x), xs);
}

Ok, that's also enough to hurt anybody's head! Let's break it down:

We have two arguments:

• Func<A, K<F, B>> f – this is the function that does the transformation to the applicative
• K<Seq, A> ta – this is the Seq<A> that is being traversed

Now let's look at the elements of the first expression. The critical part is:

Foldable.foldBack(cons, F.Pure(empty<B>()), ta)

This leverages the fact that the input type (ta) is foldable. The fold operation needs an initial state:

F.Pure(empty<B>())

F is the output Applicative - so we're lifting empty<B>() into the F applicative. empty<B> is just the constructor of an empty Seq<B>. So, F.Pure(empty<B>()) is a K<F, Seq<B>>. It should be fairly clear that this is the result type before we've processed any of the values (and indeed if the input Seq<A> is empty then this will be the result).

The function that does the folding is cons. Which is a local function below the expression:

K<F, Seq<B>> cons(K<F, Seq<B>> xs, A x) =>
    Applicative.lift(Prelude.Cons, f(x), xs);

It takes in two arguments (as all fold functions do) – the first being the running state and the second being the next item to process. We then do an Applicative.lift with the Cons function from the Prelude (which prepends an item to be the new head of a list); the mapped item (f(x)); and the list so far xs.

Applictive.lift is like calling fun(Prelude.Cons).Map(f(x)).Apply(xs) – it's a handy shortcut that makes it a little easier to lift functions.

And so, you should see that the applicative Apply method is chained for each item in the sequence. The function being applied is the Seq cons function that prepends the mapped values to the head of the list. But, if you remember (from the previous Applicative article) the Apply function has inbuilt behaviour depending on the structure being applied.

And so, if we were processing a sequence of Option values then it would know to quit if the result of f(x) is None; if we were processing a sequence of Validation values it would know to collect all of the failed values; if we were processing a sequence of Eff effects it would know to run them in parallel; etc.

This is super, super powerful and turns into incredibly concise code.

But, there's still some code from the Seq implementation of Traverse that we haven't covered:

return F.Map<Seq<B>, K<Seq, B>>(
    ks => ks, 
    Foldable.foldBack(cons, F.Pure(empty<B>()), ta));

The result of the foldBack call is mapped using Functor.Map – remember the F is an Applicative, which inherits Functor. We do this to convert from Seq<B> to K<Seq, B>. So, even though Seq<B> inherits K<Seq, B> we still can't just cast the nested K<F, Seq<B>> to K<F, K<Seq, B>> because C# just does not play nice with covariant and contra-variant casting of nested types – there were some combinations of in and out on the trait types I could use to make the above compile (without needing to Map) but they were causing runtime casting exceptions – so I decided to err on the side of caution and make the casting explicit. This adds some overhead, but is correct, which is more important. So, we need to run a map operation to get to the base interface from the concrete nested inner-type.

Here's an alternative approach that doesn't need the Map:

static K<F, K<Seq, B>> Traversable<Seq>.Traverse<F, A, B>(Func<A, K<F, B>> f, K<Seq, A> ta) 
{
    return Foldable.foldBack(cons, F.Pure(empty<B>().Kind()), ta);

    K<F, K<Seq, B>> cons(K<F, K<Seq, B>> xs, A x) =>
        Applicative.lift((b, bs) => b.Cons(bs.As()).Kind(), f(x), xs);
}

This keeps working with the abstract types all the way through the fold operation. A few things to notice compared to the original implementation:

• empty<B>() has .Kind() called on it, that turns Seq<B> into K<Seq, B>
• The updated cons function now has to convert bs to a Seq<B> (using .As()) for each item – this is converting an interface to a struct (Seq<A> is a value-type).
• Once the Cons operation is complete it has to be converted back to the base-interface using Kind()

Ultimately, this has to do multiple boxing operations per item (.As() and .Kind()) which adds more overhead than necessary. And that is why this isn't the default implementation.

It is nearly always the case that when you're traversing a collection-type, like Seq<A>, the applicative type you're mapping to is usually not a collection-type. So, doing the Map operation once (for the outer Applicative) is much more efficient than doing it on every item.

Because collections are a little more involved I wanted to present them first. Now let's look at a simpler example: Either<L, R>:

// Either Traverse
static K<F, K<Either<L>, B>> Traverse<F, A, B>(Func<A, K<F, B>> f, K<Either<L>, A> ta) =>
    ta switch
    {
        Either.Right<L, A> (var r) => F.Map(Right, f(r)),
        Either.Left<L, A> (var l)  => F.Pure(Left<B>(l)),
        _                          => throw new NotSupportedException()
    };

// Helper method to construct `Right` and cast to the underlying K type
static K<Either<L>, A> Right<A>(A value) =>
    Either<L, A>.Right(value);

// Helper method to construct `Left` and cast to the underlying K type
static K<Either<L>, A> Left<A>(L value) =>
    Either<L, A>.Left(value);

Other than the constructor functions (Left and Right) this is much simpler and should be easier to follow.

We simply pattern-match on ta which is a K<Either<L>, A> to find out what state the Either<L, A> is in:

• For the Either.Right case we invoke the f transformation function to get a resulting F applicative – we then Map the value within the Applicative and lift it into the Right constructor, leaving us with K<F, K<Either<L, B>>>.
• For the Either.Left case we want to shortcut the expression, so we don't call the f transformation function at all and instead lift the Left state into the applicative using F.Pure.

This then captures the Either short-cutting effect in the Traverse operation – we literally don't call the transformation operation at all if we're not in any state to deal with its result.

Sequence

In the previous version of language-ext there were also Sequence extension methods (for all of the types that supported Traverse. Sequence is like calling Traverse with the identity function on an already nested pair of types:

var xs = Seq(Some(1), Some(2), None);  // Nested structure
var ys = xs.Sequence();                // This line is equivalent
var zs = xs.Traverse(x => x);          // to this line.

// ys == zs

In v5 of language-ext there are three additional methods with default implementations in the Traversable trait, including Sequence:

public static virtual K<F, K<T, A>> Sequence<F, A>(
    K<T, K<F, A>> ta)
    where F : Applicative<F> =>
    Traversable.traverse(x => x, ta);

public static virtual K<M, K<T, B>> TraverseM<M, A, B>(
    Func<A, K<M, B>> f,
    K<T, A> ta)
    where M : Monad<M> =>
    Traversable.traverse(f, ta);

public static virtual K<F, K<T, A>> SequenceM<F, A>(
    K<T, K<F, A>> ta)
    where F : Monad<F> =>
    Traversable.traverseM(x => x, ta);

Sequence and SequenceM are functionally equal, just one constrains to Applicactive and the other constrains to Monad. TraverseM is the monad equivalent of Traverse.

Mostly, you'd never need to implement these yourself, but there may be some traversable types that could benefit from having bespoke overridden implementations. Specifically, collection types like Seq<A> have TraverseM implemented because it enforces sequential operations – this is useful when the applicative type you're working with is asynchronous: TraverseM enforces a serial evaluation rather than the parallel applicative behaviour – this enables the same functionality as TraverseSerial and TraverseParallel from v4 – but generalises it.

BIG NOTE: Sequence and SequenceM both take already nested types. C# doesn't like this for anything other than the nested K interface types, so Seq<Option<int>> can't be used with Sequence (compile-time error) – only K<Seq, K<Option, int>>; so if you're already in the more abstract space then Seqeunce will work, otherwise not. The workaround is to use Traverse with an identity function: xs.Traverse(x => x) – which works fine. This issue seems to just be a fundamental limitation of C# – it's extremely annoying, but at least there's a workaround.

Converting back to concrete

The result of the Traverse extension method (below) is two nested K types. Getting back to a concrete type isn't easy, because we can't just cast (as we do inside the .As() extension).

public static partial class TraversableExtensions
{
    public static K<F, K<T, B>> Traverse<T, F, A, B>(
        this K<T, A> ta,
        Func<A, K<F, B>> f)
        where T : Traversable<T>
        where F : Applicative<F> =>
        Traversable.traverse(f, ta);
        
   ...
}

Everything that works with the K type will continue to work: so using Map, Apply, etc. will 'just work'. But, obviously we want to get back to our concrete data types to use them...

To make this as painless as possible, I have found that adding a Traverse and TraverseM method to your data-type reduces the complexity of getting back to a concrete state (this is in addition to the trait-implementation of Traverse):

Here's the Traverse and TraverseM implementation for Seq<A>:

public readonly struct Seq<A>
{
    ...
    
    public K<F, Seq<B>> Traverse<F, B>(Func<A, K<F, B>> f) 
        where F : Applicative<F> =>
        F.Map(x => x.As(), Traversable.traverse(f, this));

    public K<M, Seq<B>> TraverseM<M, B>(Func<A, K<M, B>> f) 
        where M : Monad<M> =>
        M.Map(x => x.As(), Traversable.traverseM(f, this));

    ...  
}

This implementation is pretty much always exactly the same for all types, you just need to replace Seq<B> with whatever type you're implementing. So, copy-n-paste is your friend here.

What this does is map the inner-type to its concrete-type by calling .As() on it. And because this is a member of the Seq<A> type (not an extension method) it gets picked first by C# (ahead of the Traverse and TraverseM extension methods).

It still means we have a generic outer-type (K<F, ...>), but the inner-type (Seq<B>) is now concrete. This is then enough for us to call .As() on to make the whole type concrete:

var items = Seq("1", "2", "3", "X", "5");
Option<Seq<int>> values = items.Traverse(s => parseInt(s)).As();

This is a little bit of a rough edge for traversables. It's a bit more effort than the other trait types and less elegant in implementation. However, it does work without any cheating and it does turn into a truly generic system of traversables.

Breaking Changes from v4

• The 500 or so extension methods that existed before for Sequence and Traverse are now gone. The methods in the trait implementations have taken over that role. The type signatures are slightly different, with one variant of Sequence removed.
• You nearly always want to use Traverse and not Sequence – because C#'s type-system won't play nice with your nested types most of the time. Sequence is useful when the inner nested type is already in K<F, A> form.
• In pre-v5 language-ext there were Traverse extension-methods for types that can't now be supported [with the new fixed trait-interface]. And so, you may get some breaking changes where Traverse doesn't exist any more for a nested-pair of types. In reality this is unlikely, because they didn't really make much sense and were just there for completeness.
• TraverseSerial and TraverseParallel are currently deprecated. The parallelisation of the operations are now dependent on the implementation of Traverse only. However, types like Seq<A> also have a TraverseM implementation which enforces serial operations – so you can think of Traverse as parallel and TraverseM as serial.
• Because Traverse and Sequence return nested generic-types, it's not possible to make them concrete without having the same number of extension methods as before – so you'll need to call .As() to get back to your concrete type (see previous section).

Conclusion

There's no doubt that there's a couple of rough edges with traversables due to the limitations of the C# type-system. I will keep experimenting with ideas that could help improve that situation – but I won't do any hacks, I want this to use the type-system as it is.

Really, it would be nice to get some parity with the extension methods from v4, namely no issues with nested types and implicit variance casting. Luckily, everything is still totally usable, but the issues around Sequence are a little frustrating.

Even with all of that said, this version now has the bugs in Traverse and Sequence – from v4 – fixed. Because of the trait system, not in spite of it. And, you can now build your own traversable types which will instantly work with all of your foldable & applicative types and the foldable & applicative types in language-ext.

One thing that really frustrated me in the past was creating a type in my app domain that I then wanted to use with Traverse, only to remember that there was no generic traversable trait and that I'd have to implement Traverse and Sequence n-times to get the same functionality as the types in language-ext. That problem has now gone – you still need to implement Traverse for your type, but just once.

When you remember that Traverse is one of the most powerful tools in the pure-functional-programming-toolkit – it means (regardless of rough edges) we've gained some real FP superpowers here. And these superpowers can finally land in your code-base rather than just the language-ext provided types.

Next up: Monads! I promised myself I'd never write 'Yet Another Monad Tutorial' – well I guess I can't not write one now...

Part 7 - Monads.

Subscribe

This site is an independent publication launched in February 2024 by Paul Louth. If you subscribe today, you'll get full access to the website as well as email newsletters about new content when it's available. Your subscription makes this site continue to exist. Thank you!

Fresh content, delivered

Stay up to date with new content sent straight to your inbox! No more worrying about whether you missed something because of a pesky algorithm or news feed.