Higher Kinds in C# with language-ext [Part 7 - monads]

This is a multi-part series of articles – and you'll need to know much of what's in the earlier parts to follow this – so it's worth going back to the earlier episodes if you haven't read them already:

• Part 1 - Introduction, traits, semigroups, and monoids
• Part 2 - Functors
• Part 3 - Foldables
• Part 4 - Applicatives
• Part 5 - Validation
• Part 6 - Traversables

OK, this is the big one, the one we've all been waiting for, yes, it's time to implement monads!

There's a bit of a meme in the dev community around the difficulty in explaining monads. Do a search for "Yet Another Monad Tutorial" and you'll see what I mean!

Apparently, nobody has found a way to concisely or clearly describe monads to the average non-monad-knowing person. There appears to be a 'thing' where, once someone is confident with pure functional-programming, they forget how difficult/alien it seemed at first and because pure functional-programming is – in many ways – simpler than imperative programming, they lose all ability to put their minds back into that initial confused state.

You may balk at the idea that pure functional-programming is simpler than imperative programming – especially when it comes to the terms, like 'monad', 'functor', 'applicative', ... there's a feeling of "I can't place these terms with real world concepts". But, terminology aside, I have never felt more confident about my code as I have in the pure functional-programming era of my life. I did ~15 years of procedural coding (BBC BASIC and C), ~15 years of OO coding (with C++ and C#), and have now done more than a decade of FP programming (C#, F#, Haskell, PureScript). So, I feel I can confidently state that I have had enough experience to at least have an opinion on this!

I suspect I fall into the 'fail to explain properly' trap sometimes too, it's probably impossible not to. I re-read my last article on the Traversable type and can't help but think that it needs some better exposition. But, right now, I can't tell whether the five previous articles are enough for the reader to follow along – it should be, but is it?

I promised myself I'd never write a 'Yet Another Monad Tutorial'. But, because we now have the new Monad<M> trait in language-ext, it probably needs some explanation!

Yet Another Monad Tutorial

Something that is always missed in monad tutorials is "why?". Why do we even need monads?

First, we don't need them. C# devs can manage perfectly fine without them. But, what language-ext is all about is enabling pure functional programming in C#. And, although monads aren't needed for pure functional programming, they make the life of the pure functional dev easier. But, before I can explain why, let's just have a refresher on the whole pure functional programming 'thing'...

The basics of pure functional programming are this:

1. Functions are values
2. Everything is an expression
3. All expressions are pure and/or have referential transparency

Item 1, we know about, so that doesn't need explaining. Item 2, 'Everything is an expression' thing is interesting. If everything is an expression then we don't have statements – no lines of code, just an expression-tree of code. Expression trees are quite hard to mentally manage (as well as write), so we need to find a way of having lines-of-code that are still, somehow, expressions.

If you look at an ML based language, you might see some code like this:

let x = doSomething () in
let y = doSomethingElse () in
x + y

These look like statements in an imperative language, the temptation is to think the above is equivalent to:

var x = DoSomething();
var y = DoSomethingElse();
return x + y;

But, in fact they're completely different. The ML example gets rearranged by the compiler to be lambdas with invocations (everything is a function in functional programming!):

(fun x -> (fun y -> x + y) DoSomethingElse()) DoSomething()

That is how something that is an expression can end up looking like multiple statements.

There is a real scoping difference – even if they look exactly like regular statements. The example above can be factored and reduced in a way that imperative statements can't (well, not without some serious analysis).

OK, so what? Why should we care? Well, we can now write expressions in an imperative way (which I think is probably more natural for us) without losing any of the benefits of expressions.

Item 3: "All expressions are pure and/or have referential transparency" is the next thing we need in pure functional programming...

• A pure expression is either a primitive value or entirely constructed from other pure expressions. The 'smallest' pure expression is a value. It should not produce any side-effects (no mutating global state, no writing to a file, etc.).
• A pure function is one where the function body is a pure expression. The only values the expression can depend on are those provided to the function as arguments (so, no references to global state). That means the result of the function is entirely dependent on the inputs to the function.
• An expression that has referential transparency is almost exactly the same as a pure expression. The main difference is that 'internally' it may not be a pure expression (could be implemented as a for loop, for example), but on the 'outside' it behaves in exactly the same way a pure expression behaves. Namely that you could replace the expression with a value and the consequence of using it remains the same.

There is a small problem though. A requirement of both pure expressions and referentially transparent expressions is that we should be able to replace the expression with a value (because we expect the same result from evaluating the expression every single time). But, for some expressions, that isn't true...

var now = DateTime.Now;

Clearly, we can't replace the DateTime.Now expression with the first result we get and then use it forever more, otherwise the time will never change. DateTime.Now is not pure.

So, if we're going to do pure functional programming, where every single expression is pure then we need a different approach.

You may think "So what, this is C#, just use DateTime.Now and get over it?!". That is certainly a valid approach. But, you have to remember why we're doing pure functional programming in the first place:

• Fewer bugs: Pure functions, which have no side effects and depend only on their input parameters, are easier to reason about and test, leading to fewer bugs in the code-base.
• Easier optimisation: Since pure functions do not have any side effects, they can be more easily optimised by the compiler or runtime system. This can lead to improved performance.
• Faster feature addition: The lack of side effects and mutable state in pure functional programming makes it easier to add new features without introducing unintended consequences. This can lead to faster development cycles.
• Improved code clarity: Pure functions are self-contained and independent, making the code more modular and easier to understand. This can improve code maintainability.
• Parallelisation: Pure functions can be easily parallelised, as they do not depend on shared mutable state, which can lead to improved scalability.
• Composition: This is the big one. Only pure functional programming has truly effective composition. Composition with impure components sums the impurities into a sea of undeclared complexity that is hard for the human brain to reason about. Whereas composing pure functions leads to new pure functions – it's pure all the way down, it's turtles all the way down. I find it so much easier to write code when I don't have to worry about what's going on inside every function I use.

That's the 'short list', there's probably more that I've forgotten, but it's already pretty compelling.

The main thing to note is that if you opt-out of pure functional programming anywhere in an expression, then you compromise the whole expression – it stops being turtles all the way down. So, we want everything to be pure to get the compositional benefits; we need a way to encapsulate impure actions like DateTime.Now and, somehow, make them pure – otherwise we may as well give up on the idea completely.

Back to the "why?"

OK, so pure functional programming refresher done and an unresolved issue highlighted: 'encapsulation of impure expressions'.

Let's get back to the "why?". Why do we even need monads?

• Monads encapsulate impure side-effects and other effects, making them pure
  • Ding, ding!
• Monads allow sequencing of operations, like the let example earlier, so that we can chain expressions together.
• Monads (with LINQ in C#) allows us to write pure code that looks a lot like statements in imperative code.

Quite simply: Monads are the 'statements' of pure functional programming and they encapsulate messy side-effects.

And so, when you see people struggling to explain monads, or they're trying to bring them into a domain that isn't pure (or their goal isn't to enable a pure functional programming experience) then I think the reasoning in favour of monads goes awry.

Monads are simply a design-pattern for pure functional programmers. That is all. No more.

OK, that was a lot of words to say "it's a design pattern", but hopefully now you have some context for why we're even doing this.

It must be stated that, beyond the justifications above, they also encapsulate some truly awesome patterns that are not served by any other technique and they are super-powered boilerplate killers!

So, let's get back to DateTime.Now. And let's try to make that pure. What does DateTime.Now do? Well, it accesses the system-clock and uses that to give you a DateTime struct which is a snapshot of the current-time.

DateTime.Now is clearly doing an IO operation. It is accessing some state outside of the application and then returning that state. So, why don't we start by creating a type called IO<A>:

public record IO<A>(Func<A> runIO);

Notice how we're capturing a Func<A> and not a value. This is important because we're not trying to capture a snapshot but a computation.

OK, now let's create our own DateTime module (we'll call it DateTimeIO to avoid a name clash):

public static class DateTimeIO
{
    public static readonly IO<DateTime> Now =
        new (() => DateTime.Now);
}

So, now, instead of returning a DateTime we return an IO<DateTime>. This is the 'get out of jail free card', it means the return value isn't a snapshot of time any more. You can replace any call to DateTimeIO.Now with the resulting IO<DateTime> in any expression and the result will be the same. We've taken something that was impure and made it pure.

You might think that this is a sleight of hand, but it really isn't. The rules hold. We are still returning a data-structure, but it's a data representation of a computation, rather than a snapshot data-structure. The call to DateTimeIO.Now is interchangeable with IO<DateTime> in a pure expression.

The problem is that the code that wanted to use the DateTime snapshot, now can't, it has an IO<DateTime> not a DateTime – so what do we do? If you remember the discussion about lifting, this is a situation where we have a lifted computation, so we need to work in the lifted space. The first step is to make the IO<A> type into a Functor:

So, as with the examples in the previous articles, derive the type from K<F, A>:

public record IO<A>(Func<A> runIO) : K<IO, A>;

Add an extension to downcast:

public static class IOExtensions
{
    public static IO<A> As<A>(this K<IO, A> ma) =>
        (IO<A>)ma;
}

Let's also have an extension that will run the IO computation to get a concrete value:

public static class IOExtensions
{
    public static IO<A> As<A>(this K<IO, A> ma) =>
        (IO<A>)ma;

    public static A Run<A>(this K<IO, A> ma) =>
        ma.As().runIO();
}

Then we can start building the IO trait-implementation class:

public class IO : Functor<IO>
{
    public static K<IO, B> Map<A, B>(Func<A, B> f, K<IO, A> ma) =>
        new IO<B>(() => f(ma.Run()));
}

What we're doing in the Map function is invoking the Func inside the IO<A> type. It returns an A value; we pass that value to the f function, which gives us a B; and we then wrap that all inside a new Func so we can construct an IO<B>.

That means we can now work with the value within the IO<A> :

var thisTimeTomorrow = DateTimeIO.Now.Map(now => now.AddDays(1));

Hopefully it's obvious that every time we use DateTimeIO.Now we will get the latest time. That is also true if we assign DateTimeIO.Now to another variable and use that variable at some point in the future.

So, as seen in previous articles, we can lift functions into the IO functor and work with the value within.

Next, we can upgrade the IO type to be an Applicative:

public class IO : Applicative<IO>
{
    public static K<IO, B> Map<A, B>(Func<A, B> f, K<IO, A> ma) =>
        new IO<B>(() => f(ma.Run()));

    public static K<IO, A> Pure<A>(A value) =>
        new IO<A>(() => value);

    public static K<IO, B> Apply<A, B>(K<IO, Func<A, B>> mf, K<IO, A> ma) =>
        mf.Map(f => f(ma.Run()));
}

Both of these steps are needed on the way to making IO into a monad, we've done this in previous articles, so I'm pushing through quickly...

Now, let's upgrade the IO type to be a Monad:

public class IO : Monad<IO>
{
    public static K<IO, B> Bind<A, B>(K<IO, A> ma, Func<A, K<IO, B>> f) =>
        new IO<B>(() => f(ma.Run()).Run()); 

    public static K<IO, B> Map<A, B>(Func<A, B> f, K<IO, A> ma) =>
        new IO<B>(() => f(ma.Run()));

    public static K<IO, A> Pure<A>(A value) =>
        new IO<A>(() => value);

    public static K<IO, B> Apply<A, B>(K<IO, Func<A, B>> mf, K<IO, A> ma) =>
        mf.Map(f => f(ma.Run()));
}

The new function is Bind. If you look at the f function for both Map and Bind, you'll notice that the only difference is that instead of returning a B the Bind version of f returns an IO<B>.

So, monad Bind and functor Map are very similar. We can even write Map in terms of Bind and Pure:

public static K<IO, B> Map<A, B>(Func<A, B> f, K<IO, A> ma) =>
    Bind(ma, x => Pure(f(x)));

Which might give you a bit of insight into the similarities and differences between Map and Bind. The similarities are mostly aesthetic – they look similar. However, the differences are huge: by returning a new monad instead of a concrete value, we are inviting a chain of operations to happen. The implementation of Map (in terms of Bind and Pure above) highlights that Pure means 'terminate the chain'. Stop the operation here. So, Map is like a Bind operation that always terminates.

Applicative Apply can also be implemented in terms of Bind and Map:

public static K<IO, B> Apply<A, B>(K<IO, Func<A, B>> mf, K<IO, A> ma) =>
    mf.Bind(ma.Map);

Which is quite elegant and is nearly always a good first implementation of Apply, but for some monads it's better to have a bespoke Apply method.

Now, let's look at the internals of Bind a little closer:

f(ma.Run()).Run()

We get the first IO<A> – run it – then invoke f with the result. The result of f is an IO<B> which we also run. So, that's one IO operation that runs, that returns a new IO operation, which we run too.

Sounds like two operations:

doTheFirstThing();
thenDoTheNextThing();

Bind is how 'statements' are done in pure functional programming.

Let's add a few more IO values to our DateTimeIO type:

public static class DateTimeIO
{
    public static readonly IO<DateTime> Now =
        new (() => DateTime.Now);
    
    public static readonly IO<DateTime> Today =
        new (() => DateTime.Today);

    public static readonly IO<DateTime> Tomorrow =
        new (() => DateTime.Today.AddDays(1));
}

And now, let's try to use Bind:

var diff = DateTimeIO.Today.Bind(
    today => DateTimeIO.Tomorrow.Map(
        tomorrow => tomorrow - today));

So, Bind allows another IO operation inside its injected function. In theory you can do this multiple times (with any number of IO operations). But, as you can probably tell, that will turn into a pyramid-of-doom quite quickly.

You can also write the above example with two nested Bind calls and an IO.Pure:

var diff = DateTimeIO.Today.Bind(
    today => DateTimeIO.Tomorrow.Bind(
        tomorrow => IO.Pure(tomorrow - today)));

Now the terminating Pure seems more obvious!

To deal with the pyramid-of-doom we need some first-class language support. In Haskell, they deal with this using do notation, it might look something like this:

diff = do
  today    <- DateTimeIO.today
  tomorrow <- DateTimeIO.tomorrow
  pure (tomorrow - today)

Notice the pure terminator

In C# our equivalent is LINQ. It is genuine first-class monad support in C#. The only thing we couldn't do in the past with LINQ was to generalise over all monads. But, now – with the higher-kinded types in language-ext – we can. Once you have implemented the Monad<M> trait for your type, it will immediately work in LINQ (no need to manually implement Select and SelectMany):

var diff = from today    in DateTimeIO.Today
           from tomorrow in DateTimeIO.Tomorrow
           select tomorrow - today;

I often see other language ecosystems trying to bring monads into their domain. But, without first-class support for monads (like do notation in Haskell or LINQ in C#), they are (in my humble opinion) too hard to use. LINQ is the killer feature that allows C# to be one of very few languages that can facilitate genuine pure functional programming.

I just wish Microsoft would put some effort into improving LINQ:

• Discards for variable names (from _ in foo)
• Allocation free local lambdas to reduce the garbage
• Remove need to use select as the last term, allow a lifted type to be evaluated as the final term. This will allow for recursive monads that use trampolining internally (enabling infinite recursion).

So, Microsoft, please, this is your killer feature!

Pause

It's worth reviewing where we are, because we now have a fully fledged IO monad (and applicative, and functor!) with just this code:

public record IO<A>(Func<A> runIO) : K<IO, A>;

public static class IOExtensions
{
    public static IO<A> As<A>(this K<IO, A> ma) =>
        (IO<A>)ma;

    public static A Run<A>(this K<IO, A> ma) =>
        ma.As().runIO();
}

public class IO : Monad<IO>
{
    public static K<IO, B> Bind<A, B>(K<IO, A> ma, Func<A, K<IO, B>> f) =>
        new IO<B>(() => f(ma.Run()).Run());

    public static K<IO, B> Map<A, B>(Func<A, B> f, K<IO, A> ma) =>
        Bind(ma, x => Pure(f(x)));

    public static K<IO, A> Pure<A>(A value) =>
        new IO<A>(() => value);

    public static K<IO, B> Apply<A, B>(K<IO, Func<A, B>> mf, K<IO, A> ma) =>
        mf.Bind(ma.Map);
}

I spent a lot of time in earlier versions of language-ext building code-gen solutions to make it easy to generate monadic types. And now, without any code-gen, we have a much more powerful system that you can build by hand. Very cool!

Naming

Some other 'Yet Another Monad Tutorial' writers have tried to avoid using the word 'monad', or have introduced it at the end of the tutorial, or have renamed the concept entirely.

Personally, I believe if you're going to come along for the 'pure functional ride', then you need to know how to communicate with other people in the space; as well as be able to search online for further information on the subject. And that mostly means understanding the lexicon of Haskell, Scala, PureScript, etc. There's a common dialect and I think sticking with it, even if the words sometimes feel ugly, is the right way to go.

But, if it helps, here are some approachable names that might help give a more instinctive understanding:

• Chainable instead of Monad – to represent the fact that operations are chained serially.
• AndThen or Then instead of Bind

Composition

In the article on Validation – which was an extended discussion of Applicatives – there is a diagram (repeated below) that has lower-kinds at the bottom, higher-kinds above and the various functions (arrows) that map between the types.

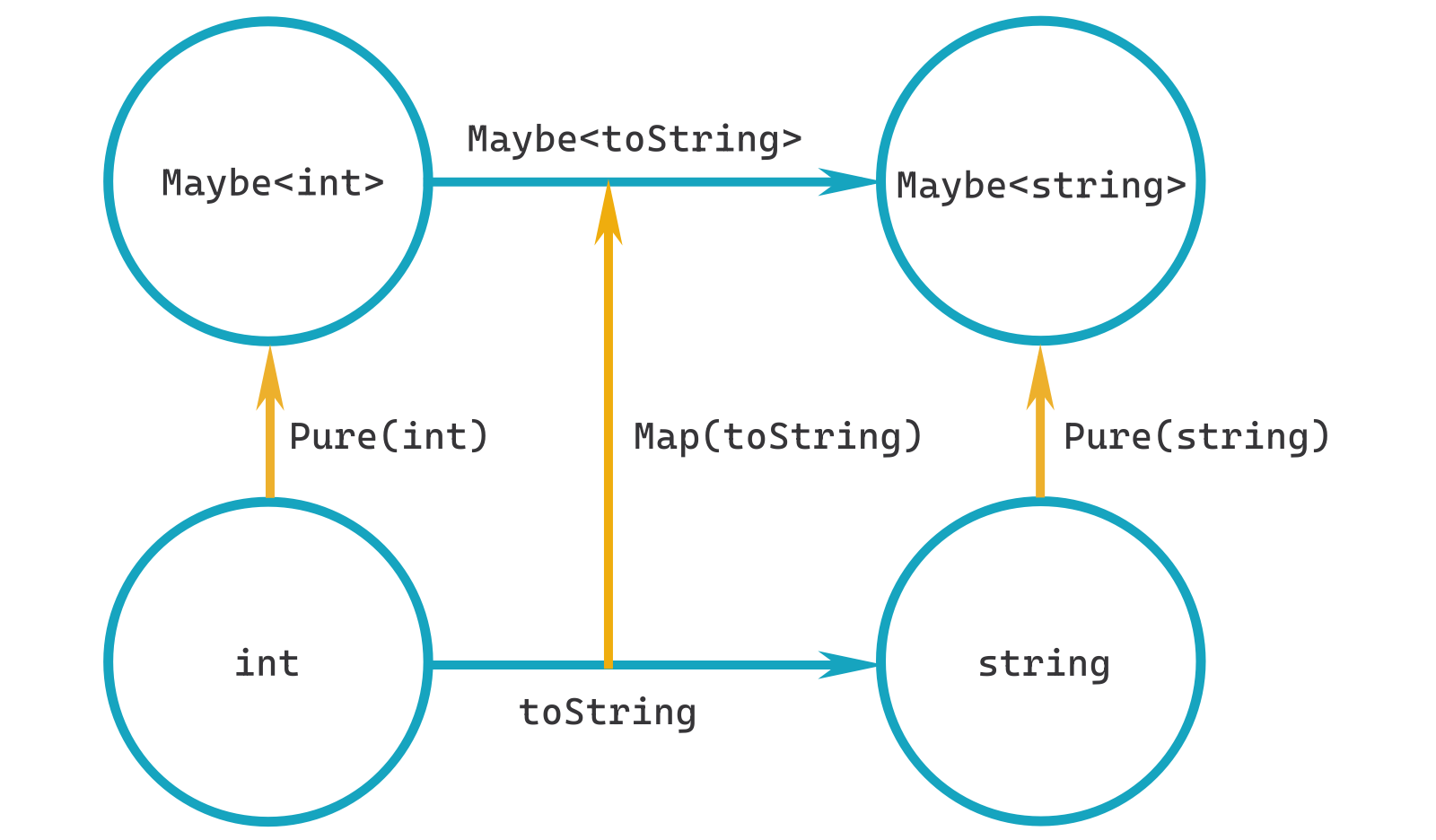
• The bottom toString arrow is saying: "If you provide an int, I will give you a string in return" (basic function invocation).
• The top Maybe<toString> arrow is saying "If you provide a Maybe<int>, I will give you a Maybe<string> in return" (applicative Apply)

So, if you follow the arrows we have various composition options:

• int -> Maybe<int> -> Maybe<string> which composes to int -> Maybe<string>
• int -> string -> Maybe<string> which also composes to int -> Maybe<string>
• int -> string
• Maybe<int> -> Maybe<string>
• int -> Maybe<int>
• string -> Maybe<string>

These arrows and compositions give us the full set of transformations for each of the types in the diagram. They also hint at potential optimisations: if there are two routes that start and end in the same place, which one is more efficient?

What we don't have is any way to get from:

• Maybe<int> -> int
• Maybe<string> -> string

Because there are no arrows there to follow. Do we need them? And do they make sense?

Usually, going from higher-kinds to lower-kinds is a destructive action. For example, to make Maybe<int> (equivalent of Option<int> in language-ext) collapse down to an int would require us to have a default value to use in case the type is in a Nothing (None) state.

These types of 'lowering' functions are type-specific and don't have abstractions that we can discuss. For discriminated-union types the function is usually a pattern-match operation that collapses the union down to a non-union type. So, we'll consider that to not be an option for trait-level programming.

However, lowering optionally to work on the values within the type, to then re-lift into the higher space is possible. And that is the Bind function...

If we look at the Monad trait we can get some clues:

public interface Monad<M> : Applicative<M> 
    where M : Monad<M>
{
    public static abstract K<M, B> Bind<A, B>(K<M, A> ma, Func<A, K<M, B>> f);

    // default implementations removed for clarity
}

So, we have an argument called ma which is of type: M<A>. That is a 'structure' with zero or more A values within – from the outside we have no idea what's inside – but that doesn't matter, the implementation of the Bind function knows what's inside.

The Bind implementation must extract the A value(s) so that it can pass them to the function f which in return gets us an M<B>.

Or, more concisely:

M<A> -> A -> M<B>

So, the effect of the Bind action is to zig-zag between higher and lower kinds.

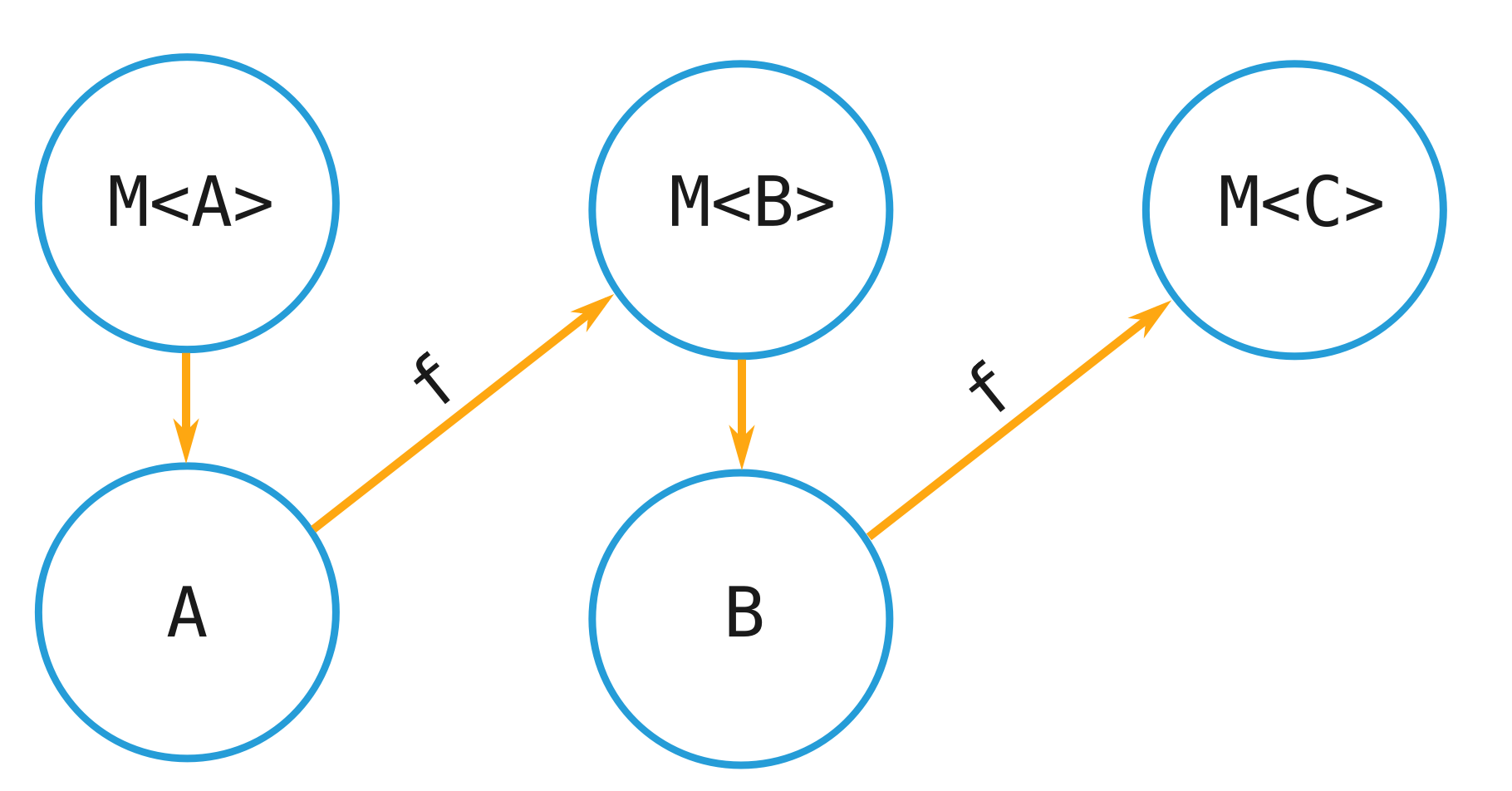
The 'lowering' arrows (those pointing down) are the bespoke behaviour of the monad. If it's an IO monad then it knows how to run the internal Func<A> computation that extracts the A value. If it's an Option<A> monad then it does a check to make sure that the structure is in a Some state, and if so it yields the value.

So, why can't the lowering arrow be used to create a generalised lowering function? Because the higher-kind might not actually have any values within it. Option<A> might be None, so we can't yield an A. But, we can map Option<A>.None to Option<B>.None – because we can pluck a None out of thin air. That allows the 'contract' of Bind to be honoured: M<A> -> M<B>,

This is also the essence of the short-cutting behaviour of monads. If there's no value to yield then the f function passed to Bind never gets called because we have no value to give it!

And, because we know that monads chain expressions together serially; not calling f means the rest of the expression isn't invoked either. We essentially exit out of the computation early.

There's another common phrase used to describe monads: "programmable semicolons". Although it is slightly misleading, you can see the lowering-arrow as the point between two computations (two statements) where additional logic lies. This logic can do lots of different things. In the case of Option it is effectively a 'null check' to see if we even have a value – and if not, it bails out of the computation.

Let's take a look at two examples using Option from language-ext:

var inp1 = "100";
var inp2 = "200";
var inpX = "NUL";

var res1 = from x in parseInt(inp1)
           from y in parseInt(inp2)
           select x + y;

var res2 = from x in parseInt(inp1)
           from y in parseInt(inpX) // fails to parse, `y` is never assigned
           from z in parseInt(inp2) // never executes
           select x + y + z;        // never executes

// res1 == Some(300)
// res2 == None

The parseInt function returns an Option<int> and it will be None if the parse fails.

On the first example, everything parses correctly, which means the final x + y is run.

On the second example, the parseInt(inpX) will return None which means the we have no value to assign to y. And therefore we must exit, because the rest of the expression depends on y having a valid value.

If we look at the implementation of Bind for Option we can see this short-cutting behaviour:

static K<Option, B> Bind<A, B>(K<Option, A> ma, Func<A, K<Option, B>> f) =>
    ma.Match(
        Some: x => f(x),
        None: Option<B>.None);

We pattern-match on the Option, if we're in a Some state then we call the f function that continues the expression. If we're in a None state, we just return None – halting the expression.

It's remarkably simple really, but extremely effective because this won't allow you to continue unless we have a value. It can't be cheated. You can't make a mistake when using Option – whereas similar if checks for null values (or the accidental absence of them) can lead to major bugs.

Another interesting aspect of Option<A> is that it helps us fulfil our pure functional programming mandate. Remember, we shouldn't have any side-effects in our functions or expressions. Exceptions are side-effects. Really, if method-signatures in C# were honest, we'd never have a return type of void. And methods that throw exceptions might look something like this:

(Exception | int) ParseInt(string value)

Exceptions should be for truly exceptional events that you can't recover from. Exceptions should not be thrown for expected errors – a failure to parse is expected for a parsing function.

I saw an interesting post the other day on Twitter, from a PM on the .NET team at Microsoft, he was lamenting the incorrect usage of ArgumentException – and then giving advice on what should be done. Completely oblivious to the fact that exceptions are just the wrong approach. The system clearly isn't working as intended; and that's because there's no compiler support, there's no type-system support, it's just convention.

I find it crazy that something like that even needs to be written. The correct approach is to make your function total – that means for every combination of values provided to the function as arguments there should be an associated value in your return type: every value in your domain should map to a value in your co-domain. This honours the requirement for the output of a pure function being totally dependent on its inputs.

How do we do this?

• Constrain the types that are used for the arguments. Make sure there's no possibility of constructing input values that are 'out of range'.
• Where the input arguments are constrained as much as possible, but the combined states of all arguments still falls outside of what the co-domain can handle, augment the co-domain with a failure value. This is where Option<A> comes in. It allows us to return None if we're unable to handle the input values: we augment the co-domain.

This leads to declarative type signatures like below. Type signatures that speak to programmers:

Option<int> parseInt(string value)

Monads are a big part of the declarative programming story. They 'mark' whole sections of code as having a particular flavour. For example, once you're working in the IO monad you have declared that code as something that 'does IO'. I know that might sound obvious, but it encourages you to separate your non-IO code from your IO code, which leads to more composition options, and ultimately more robust code.

By the way, this is why you shouldn't ever really call .Run() on the IO monad (well, not externally, internal behaviours like Map and Bind are fine). Once you're in an IO lifted space you should stay there to indicate the expression 'does IO'. The place to call Run is once in your Main function. Although, because we sometimes need more flexibility in C#, once in your web-request handler also makes sense. Collapsing IO<A> down to A re-injects your code with impure effects, breaking the pure functional programming mandate.

So far we've seen that:

• The Bind function for the IO<A> monad allows us to make impure operations, pure.
• The Bind function for the Option<A> monad allows us to deal with functions that might not be able to return a value (partial function) and, if no value is available, the Bind function automatically short-cuts the expression to stop accidental usage of None values.

The behaviour of the two Bind functions are dramatically different to each other, yet they share the same abstraction: they're both monads.

It turns out there are many different 'flavours' of Bind function that can be written that cover a whole slew of behaviours; from resource-tracking, state-management, configuration, logging, validation, list iteration, stream-processing, etc. etc. They're all just different implementations of Bind. I think this is another reason why Yet Another Monad Tutorials are quite hard to write: there's so much that you can do.

If you can program your semicolons, where's the limit!? How could you possibly write a tutorial that covers it all?

Ultimately, the Bind function is just another form of function composition. The result of the composition is: M<A> -> M<B>. Where M is the flavour of monad.

Everything in functional programming is function composition. E v e r y t h i n g. Monads are just another flavour of function composition that works with slightly different arrows to the other flavours! I know the abstractions are sometimes a bit hard to picture, but often it just means lining up the types and following the arrows. In many ways it ends up being more like Lego than programming!

This article is now probably one of the longest so far (with the fewest code examples); I realise there were a number of diversions into 'the why' of pure functional programming, but I feel that is the real origin-story of monads and why you should care about them.

That has made this article a bit longer and wordier, but hopefully it sets the scene nicely for the next episode. In the next article we'll dig into the different types of monad in language-ext and also discuss monad 'join', also known as Flatten.

Part 7: Monads

Subscribe

This site is an independent publication launched in February 2024 by Paul Louth. If you subscribe today, you'll get full access to the website as well as email newsletters about new content when it's available. Your subscription makes this site continue to exist. Thank you!

Fresh content, delivered

Stay up to date with new content sent straight to your inbox! No more worrying about whether you missed something because of a pesky algorithm or news feed.